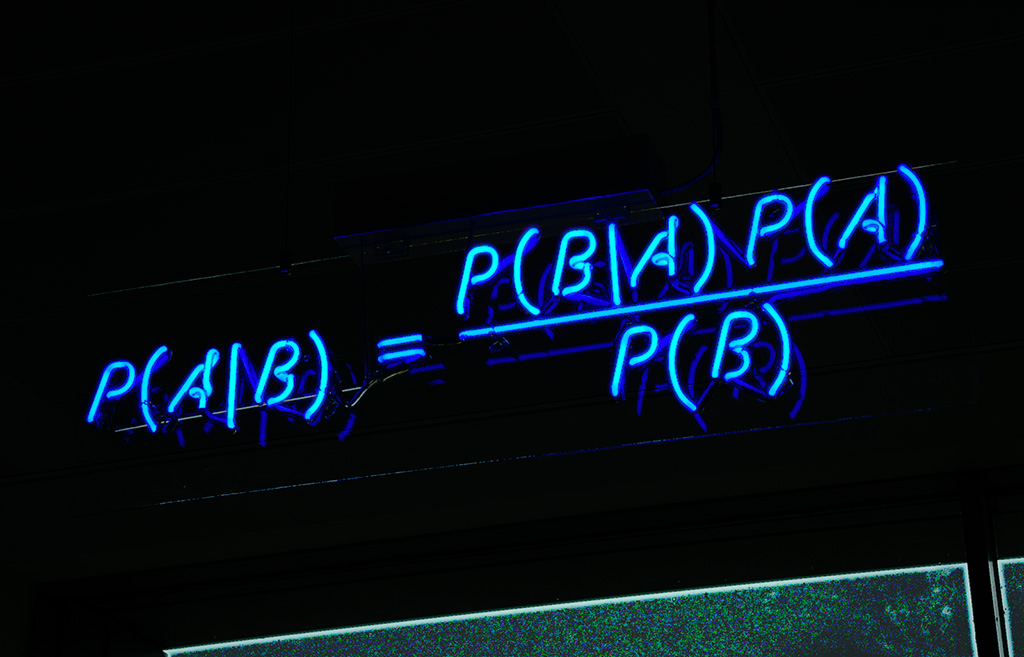La méthode de Monte Carlo, pierre angulaire de la science computationnelle moderne, est née au milieu des années 1940, catalysée par la convergence de deux événements monumentaux : le développement du premier ordinateur électronique (ENIAC) et l’émergence de la recherche nucléaire à Los Alamos. Le nom de la méthode, proposé par Nicholas Metropolis, fait allusion au célèbre casino de Monte Carlo, soulignant ainsi les fondements de la méthode dans l'aléatoire et la probabilité.
La notion de parcimonie joue un rôle transverse en TSI puisqu’elle permet d’aborder des tâches en apparence aussi diverses que la compression, le débruitage, la séparation de sources, l’acquisition compressée, et plus généralement les problèmes inverses. Un vecteur est dit parcimonieux si la plupart de ses coordonnées sont nulles. Un vecteur avec une telle propriété est naturellement compressible, puisqu’il peut être décrit en indiquant simplement les quelques indices associés à des coordonnées non nulles, ainsi que les valeurs de ces coordonnées.
Née dans les années cinquante du siècle dernier, la théorie des matrices aléatoires de grandes dimensions a été conçue à l'origine pour répondre à certaines questions de physique mathématique. Constituée depuis en branche propre des mathématiques, elle connaît aujourd'hui un développement foisonnant et trouve des applications dans de nombreux domaines scientifiques tels l'analyse des systèmes quantiques désordonnés, la théorie des nombres, l'économétrie ou les réseaux biologiques. Dans les années quatre-vingt-dix, elle a fait son entrée dans le domaine du signal et des communications. Plus récemment, elle a trouvé de nombreuses applications en théorie de l'apprentissage.
Il faudrait bien plus que quelques pages pour retracer l’histoire de l’analyse temps-fréquence et rendre justice à son développement dans ses multiples ramifications. Quelques rares textes existent en ce sens, comme la monographie [19] qui conduit son propos jusqu’aux lisières de l’analyse en ondelettes, dont l’importance va bien au-delà de son interprétation temps-fréquence. Le choix fait ici est de se concentrer sur les aspects proprement temps-fréquence (à la Wigner, Ville ou Gabor, pour faire court) en s’arrêtant au début de la période contemporaine dont on peut dater le tournant à l’orée des années 80, période qui correspond aussi à l’émergence et la montée en puissance des ondelettes.
Le cerveau et le système nerveux constituent des modèles de choix pour le traitement de l’information dont il serait judicieux de s’inspirer. Les premiers essais de modélisation du Neurone datent de 1943. Quinze ans plus tard, est apparu le Perceptron, qui a ouvert la voie aux Réseaux de Neurones Artificiels (RNA). Il s’en suit une période sombre jusqu’à la fin des années 70 où un regain d’intérêt s’est manifesté dans la communauté scientifique, avec, entre autres, les cartes de Kohonen, le perceptron multi-couches, la machine de Boltzmann, et bien d’autres. Plus récemment, sont apparus les réseaux convolutifs et le « Deep Learning » avec Yann Le Cun. C’est alors l’explosion d’une nouvelle voie de recherche en Intelligence Artificielle, avec des performances impressionnantes dans de multiples domaines d’application (reconnaissance des visages, traduction automatique, robotique autonome, médecine, génome, …).
Le principe des communications numériques est de transmettre des signes en nombre fini à des instants discrets. En pratique on transmet des trames d’une certaine longueur N successivement. Ainsi cette trame peut être vu comme un vecteur dont les coordonnées sont les signes discrets à transmettre.
La résolution de problèmes inverses permet de remonter à l’information originale d’un objet d’étude à partir d’observations dégradées de ce même objet. La généralité et la cohérence de l’approche inverse permet de traiter de façon globale et avec des méthodologies similaires des données de nature très différentes (images 2D ou 3D, images hyper-spectrales), voire hétérogènes. En TSI, les applications phares de ce domaine d’étude sont la microscopie, l’astrophysique, ou l’imagerie médicale.
L’inférence bayésienne constitue une branche des méthodes statistiques d’estimation. Elle vise ainsi à déterminer des quantités d'intérêt à partir de mesures capteurs entachées d'erreurs. Sa particularité est que les paramètres inconnus sont probabilisés : outre l’information apportée par les observations, les méthodes bayésiennes s’appuient donc également sur des connaissances a priori. Les estimateurs sont construits à partir de la loi a posteriori, obtenue en appliquant la règle de Bayes.
La vision par ordinateur analyse les images acquises par une ou plusieurs caméras afin d’extraire des informations sur la scène filmée telles que la reconstruction 3D, la localisation des caméras, la reconnaissance d’objets... Elle a pour objectif de donner une intelligence au système d’acquisition se rapprochant de la vision humaine. Cette discipline apparait véritablement en 1963 avec les travaux de thèse de Lawrence Roberts dans lesquels il décrit comment extraire la forme 3D d’un solide à partir d’images 2D. Il s’ensuit un réel enthousiasme vers la recherche d’un système expert imitant la vision humaine pour lequel les efforts furent rapidement vains au regard de la technologie de l’époque.
La thématique Sécurité des données multimédia est intégrée actuellement au sein du GDR ISIS dans l’action Sécurité et données multimédia de l’axe 1 du thème D (Compression, Protection, Transmission) du GDR ISIS.
Dans cette thématique il est abordé la problématique de sécurisation des données visuelles pendant leur transmission, leur archivage, leur partage et leur visualisation. D’après CISCO, les données visuelles (images, vidéos, objets et scènes 3D) représentent plus de 80% du trafic Internet mondial en 2020. Avec le tout numérique, il devient de plus en plus facile de copier des données, de les visualiser sans droit, de se les approprier, mais aussi de les falsifier ou de détourner leur fonction primaire.
Lors de communications sur un canal de propagation (fibre optique, atmosphère dans le cas des réseaux cellulaires), le signal transmis subit des modifications qui pourront conduire à une mauvaise détection des données émises, bref, des erreurs vont se produire sur les données. Il a été remarqué qu’en introduisant des relations internes entre les données à émettre, on peut à la réception détecter la rupture de ces relations en cas d’erreur de transmission et en partie reconstruire ces relations pour corriger les erreurs. Cette problématique très vaste a donné naissance à la notion de code correcteur d’erreur (en anglais, channel coding). Evidemment de multiples manières existent pour créer ces relations internes.
