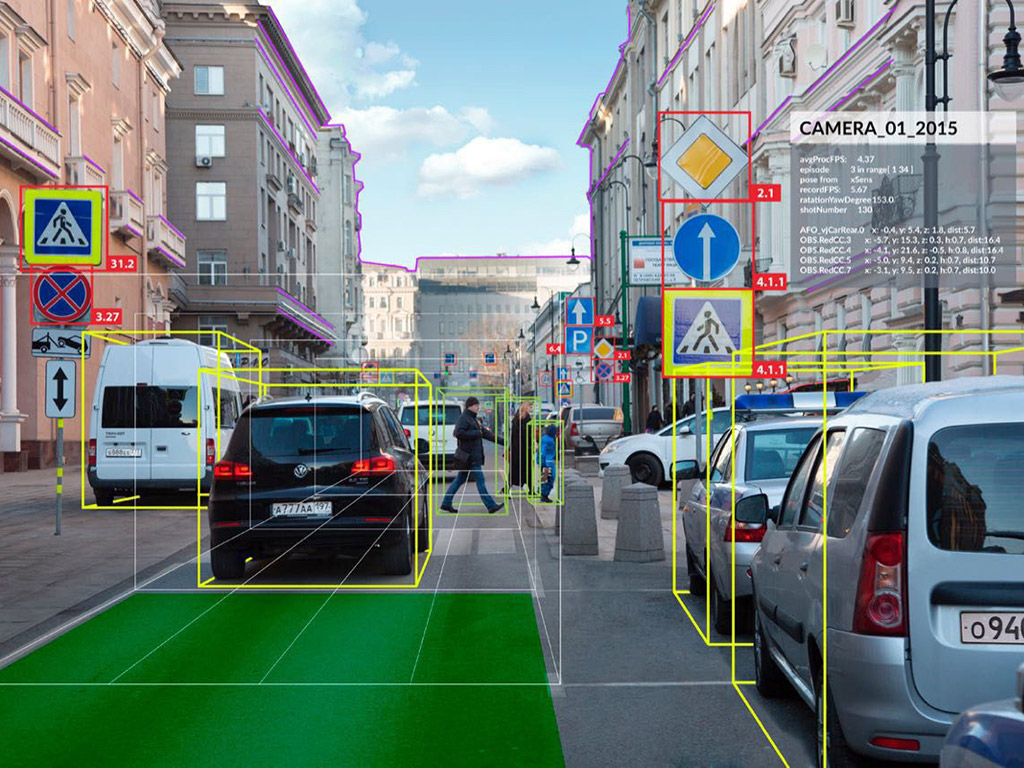
Lors de communications sur un canal de propagation (fibre optique, atmosphère dans le cas des réseaux cellulaires), le signal transmit subit des modifications qui pourront conduire à une mauvaise détection des données émises, bref, des erreurs vont se produire sur les données.
Il a été remarqué qu’en introduisant des relations internes entre les données à émettre, on peut à la réception détecter la rupture de ces relations en cas d’erreur de transmission et en partie reconstruire ces relations pour corriger les erreurs
Cette problématique très vaste a donné naissance à la notion de code correcteur d’erreur (en anglais, channel coding).
Evidemment de multiples manières existent pour créer ces relations internes. La plus naturelle est de considérer un ensemble de données auxquelles on adjoint des relations linéaires entre elles. On parle alors de code linéaire en bloc (le plus souvent binaire au sens où les données sont des 0 ou des 1). Le plus simple est le code à répétition ou le code de parité (qui consiste à rajouter un 0 si l’ensemble des données binaires donne un résultat pair ou un 1 si le résultat est impair). Depuis le premier code proposé par Hamming [1], de nombreuses propositions ont été faites comme les codes BCH (Bose, Chaudhuri, Hocquenghem) [2,3], les codes de Reed-Solomon pour gérer des erreurs successives les rendant très populaires [4], jusqu’à encore très récemment les codes polaires [5].
D’autres types de code existants comme les codes convolutifs [6] qui mélangent les codes en bloc linéaires avec une opération de convolution linéaire. Ces codes sont utilisés dans pratiquement tous les systèmes actuels.
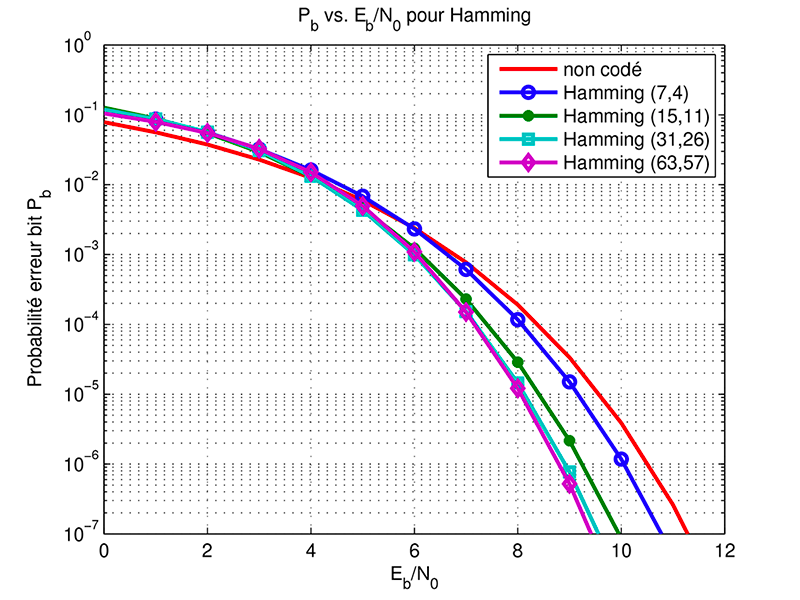
Néanmoins, il est connu que théoriquement pour avoir de bonnes performances, les codes doivent être longs [7], c’est-à-dire, qu’ils doivent considérer un ensemble de données le plus grand possible. Ceci induit généralement un décodage très complexe. Une équipe de l’IMT Atlantique (Telecom Bretagne à l’époque) a eu l’idée d’associer deux codes de longueur standard de manière élégante, pour obtenir un code dit « turbo-code », et de proposer un décodeur innovant dit itératif efficace dans les années 90 [8]. Ce fut le point de départ d’une nouvelle branche d’algorithme de réception dit itératif qui a connu des succès immenses par la suite. Juste après cette découverte, d’anciens codes en bloc dénommés LDPC (Low Density Parity Check Codes) et imaginés dans les années 60, indécodables à l’époque, ont été revisités [9]. Ces deux familles de codes font partie des standards actuels.
En fait avant même de protéger les données pour les transmettre, on peut les manipuler afin de les rendre moins gourmandes en espace de stockage et donc en quantité de données à transmettre. Cette problématique a pour nom le « codage de source » ou compression des données. Cette compression des données peut être effectuée sans ou avec perte d’information. Dans le cadre sans perte d’information, la méthode la plus connue est le codage de Huffmann [10] qui grossièrement attribue un plus petit nombre de bits aux signes les plus fréquents et un plus grand nombre de bits aux signes les moins fréquents afin d’avoir la moyenne du nombre de bits par séquence de signes plus petite que le logarithme (en base 2) du nombre de signes. Dans le cadre avec perte d’information, les manières de procéder sont très dépendants du type de données. Si les données sont sonores on songera au MP3, si elles sont visuelles, on songera à JPEG (Joint Photographic Experts Group), etc. Le détail de toutes ces manières dépasse largement le cadre de ce texte dédié aux codes correcteurs d’erreur.
Une question naturelle se pose : quel est le taux de compression maximal ? lors d’une transmission, quel est le nombre de bits maximal qu’on peut transmettre par instant discret sans erreur ? Et si ces valeurs existent, en sommes-nous loin avec les algorithmes actuels ? La réponse aux deux premières questions a été apporté par C. Shannon en 1948 pour une transmission avec un unique utilisateur n’utilisant qu’une seule antenne [7].
Références
[1] R. Hamming, Error-detecting and error-correcting codes Bell Syst. Tech. J., 1950.
[2] R. Bose et D. Ray-Chaudhuri, On a class of error-correcting binary group codes, Inform. Control,
1960.
[3] A. Hocquenghem, Codes correcteurs d'erreurs, 1959.
[4] I. Reed, G. Solomon, Polynomial codes over certain finite fields, J. Soc. Indus. Appl. Math., 1960.
[5] E. Arikan, Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric
Binary-Input Memoryless Channels, IEEE Transactions on Information Theory, 2009.
[6] P. Elias, 1954.
[7] C.E. Shannon, A Mathematical Theory of Communication, Bell System Technical Journal, 1948.
[8] C. Berrou, A. Glavieux et P. Thitimajshima, Near Shannon limit error-correcting coding and decoding,
IEEE International Conference on Communications, 1993.
[9] R. Gallager, Low Density Parity Check Codes, 1963.
[10 D. Huffman, A method for the construction of minimum-redundancy codes, Proceedings of the I.R.E., 1952.