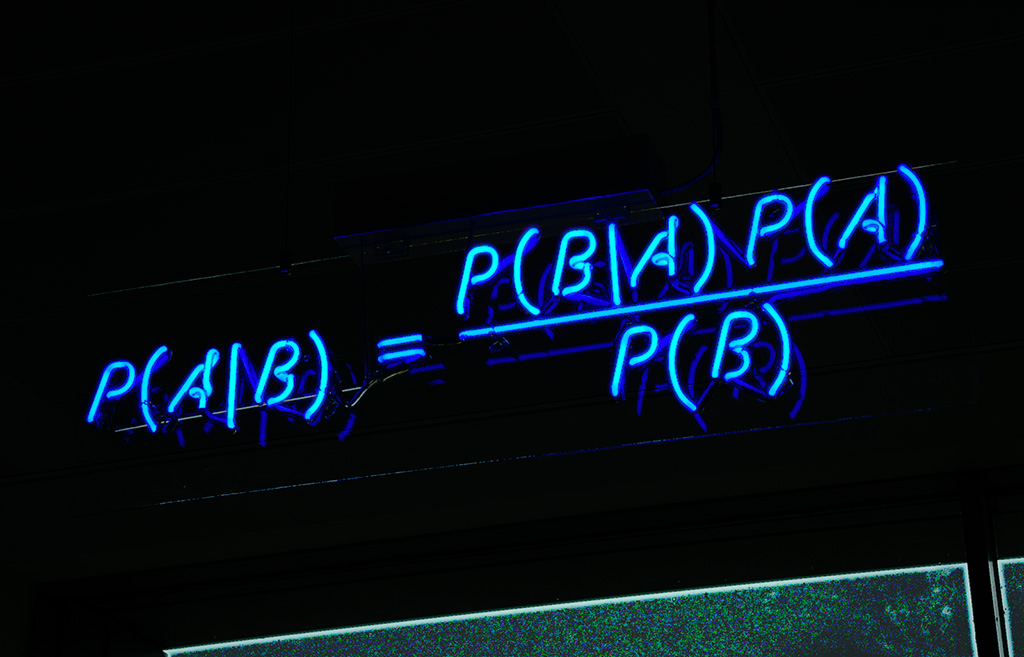La notion de parcimonie joue un rôle transverse en TSI puisqu’elle permet d’aborder des tâches en apparence aussi diverses que la compression, le débruitage, la séparation de sources, l’acquisition compressée, et plus généralement les problèmes inverses.
Un vecteur est dit parcimonieux si la plupart de ses coordonnées sont nulles. Un vecteur avec une telle propriété est naturellement compressible, puisqu’il peut être décrit en indiquant simplement les quelques indices associés à des coordonnées non nulles, ainsi que les valeurs de ces coordonnées.
Plus généralement, les techniques de compression en ondelettes développées dans les années 90 s’appuient sur le fait qu’on peut obtenir de très bonnes approximations des signaux réguliers par morceaux avec des combinaisons linéaires d’un faible nombre d’ondelettes. Lorsqu’un tel signal est contaminé par du bruit additif Gaussien, on peut aussi exploiter cette propriété de parcimonie pour le débruiter, en seuillant les coefficients d’ondelettes du signal bruité pour ne garder que les plus grands avant de procéder à la transformée en ondelettes inverse. Comme établi par D. Donoho et I. Johnstone [1], un tel procédé de débruitage possède des propriétés de quasi-optimalité statistique.
Une avancée majeure, qui ouvre la voie à tout un pan de travaux exploitant la parcimonie pour les problèmes inverses et l’échantillonnage compressé (nous y reviendrons), est le passage de représentations de signaux dans des bases (souvent orthogonales) à des représentations dans des familles redondantes, appelées dictionnaires [2], et dont les éléments sont appelés des atomes. Alors que la représentation d’un vecteur comme combinaison linéaire d’éléments d’une base est toujours unique, il y a une infinité de représentations dans un dictionnaire : cela offre en effet une flexibilité accrue pour choisir une représentation aussi propice que possible à la tâche considérée (compression, débruitage …). L’idée d’exploiter de tels dictionnaires redondants pour calculer des approximations non-linéaires, ou des décompositions atomiques, apparaît dans les années 90 en TSI sous deux formes complémentaires : dans le travail de S. Mallat et Z. Zhang sur Matching Pursuit [2], et dans celui de S. Chen et D. Donoho sur Basis Pursuit [3].
Matching Pursuit –de même que sa variante Orthonormal Matching Pursuit (OMP), présente en filigrane dès le travail de S. Mallat et Z. Zhang– est un algorithme qui sélectionne itérativement des atomes pour minimiser l’erreur résiduelle. Cette approche gloutonne est inspirée de Projection Pursuit [4], une technique de régression introduite en statistiques par J. Friedmann et J. Tukey dans les années 70 également très liée à l’algorithme CLEAN de J. Högborn pour la déconvolution en radio-astronomie [5]. Laurent Jacques mentionne aussi dans une note de blog [17] des travaux des années 30 où des idées similaires apparaissent pour résoudre « à la main » de façon approchée des systèmes linéaires, avant l’apparition des premiers ordinateurs programmables.
Plus qu’un algorithme, Basis Pursuit (ainsi que son jumeau LASSO, introduit de façon quasi-concomitante en statistiques par R. Tibshirani [6]) formule la sélection d’atomes de façon indirecte comme un problème convexe de minimisation de norme L1 –une idée alternative aux moindres carrés qu’on trouve déjà dans les travaux de J. Claerbout et F. Muir [7] dans les années 70– et nécessite donc de faire appel à des algorithmes d’optimisation sur lesquels nous reviendrons. En présence de bruit, Basis Pursuit denoising formule un problème de minimisation comportant deux termes : un terme d’attache aux données quadratique, auquel s’ajoute un terme de pénalité L1 dont il faut régler le poids. Étant donné un vecteur z et une matrice A, le problème idéalisé de représentation parcimonieuse consiste à chercher le vecteur x le plus parcimonieux tel que z = Ax. Des variantes existent dans le cas de représentations approchées, mais bien que l’on réalise vite que tous ces problèmes sont essentiellement combinatoires et NP-difficiles [8], le comportement empirique de Basis Pursuit et de Matching Pursuit ne manque pas d’intriguer [3] : dans un cadre synthétique où un signal est généré à partir d’une représentation parcimonieuse « de référence » x_0 sous la forme z = Ax_0, ces approches sont souvent capables de retrouver exactement ladite représentation. Ces phénomènes empiriques sont rapidement exploités en séparation de sources, avec notamment la notion d’analyse en composantes parcimonieuses ou morphologiques. L’idée générale est que si on observe la superposition z = z_1+z_2 de deux signaux admettant chacun une représentation parcimonieuse, z_i = A_i x_i, alors sous des conditions empiriquement favorables on peut identifier x_1, x_2 (et donc reconstruire z_1, z_2) en cherchant la représentation la plus parcimonieuse de z = [A_1 , A_2] [x_1 ; x_2].
Le deuxième jalon clé du domaine est, au début des années 2000, la caractérisation des premières conditions formelles garantissant l’identification de représentations parcimonieuses via le principe de minimisation L1 [9] ou via l’algorithme OMP [10]. Il semble que ce soit aussi le moment où émerge la notion de « pseudo-norme » L0 d’un vecteur z : cette « norme » correspond simplement au nombre de composantes non nulles de z, et la notation coïncide avec les classiques normes Lp avec la convention que pour t=0 on a t^0 = 0, tandis que t^0 = 1 pour t>0.
On peut raisonnablement supposer que la mise en lumière des garanties de reconstruction parcimonieuse par régularisation L1 –avec des techniques déjà présentes dans les travaux précurseurs de Jean-Jacques Fuchs [11]– joue un rôle d’aiguillon pour motiver le développement d’algorithmes proximaux (voir l’article d’histoire sur les Problèmes Inverses) [12]. Ces algorithmes rendent facilement accessible la minimisation L1, jusqu’alors réservée aux experts car nécessitant de faire appel à de coûteux algorithmes génériques de programmation linéaire ou quadratique, avec des paramètres complexes à régler. Les premières garanties en reconstruction parcimonieuse sont vite améliorées et étendues, elles donnent par ailleurs un cadre théorique et algorithmique flexible et solide dont le déploiement couvre une large gamme de problèmes inverses sous-déterminés. Enfin, une conséquence majeure des garanties de reconstruction sous hypothèse de parcimonie est l’apparition du concept d’échantillonnage compressif (terminologie due à Donoho [13] pour des idées –notamment l’échantillonnage aléatoire dans le domaine de Fourier– attribuées au travaux pionniers de Candès-Romberg-Tao [14]). Il s’agit de s’affranchir des contraintes inhérentes aux problèmes inverses linéaires classiques, dans lesquels la matrice A est en quelque sorte subie et peut avoir des caractéristiques défavorables, limitant de facto les niveaux de parcimonie pour lesquels des garanties de reconstruction sont possible.
L’idée centrale de l’échantillonnage compressif, est la suivante : quand on conçoit un dispositif physique pour effectuer des mesures linéaires de signaux analogiques (par exemple, un radiotélescope, ou un scanner IRM …), pourquoi ne pas profiter des degrés de liberté dont on dispose pour s’assurer que la matrice correspondante ait de bonnes propriétés vis-à-vis de la régularisation parcimonieuse ? L’échantillonnage comprimé consiste ainsi à guider la conception du dispositif d’acquisition des données, modélisé par A, pour en améliorer les performances de reconstruction sous hypothèse de parcimonie et réduire significativement les temps ou les coûts d’acquisition.
De façon a priori surprenante, l’optimisation des propriétés de A passe par l’exploitation volontaire d’aléa dans sa conception, un principe qui a une longue histoire en informatique théorique – depuis les travaux pionniers de Ph. Flajolet jusqu’à ceux de A. Gilbert, Y. Avridis, S. Muthukrishnan et M. Strauss [15], qui ont de fait directement inspiré le développement de l’échantillonnage compressif – mais aussi en imagerie par rayons X avec les techniques de masques à ouverture codée [16]).
La parcimonie prend aujourd’hui de nombreux visages nouveaux. L’idée explicite de vecteurs parcimonieux dans un domaine connu (par exemple en ondelettes) ou inconnu (via la notion d’apprentissage de dictionnaire) a ainsi donné place à de nombreux avatars modernes, pour rendre compte d’une diversité de connaissances a priori sur les données allant de la parcimonie structurée à la parcimonie continue ou aux modèles de rang faible. Dans tous les cas, il s’agit en essence de capturer la faible dimension intrinsèque d’un modèle structuré de données : même si celles-ci sont au premier abord dans des espaces de très grande dimension, il existe souvent des indices comme quoi elles peuvent être exprimées avec un nombre réduit de paramètres ou degrés de liberté.
Identifier des algorithmes efficaces pour projeter des données arbitraires sur ces modèles de faible dimension est aujourd’hui l’un des principaux enjeux pour exploiter de tels modèles dans le cadre du débruitage, de la séparation de sources, des problèmes inverses et de l’échantillonnage compressif. Les réseaux de neurones, et les versions déroulées des algorithmes proximaux, offrent pour cela des directions de recherche qui semblent très prometteuses.
Références
[1] David L. Donoho & Iain M. Johnstone, "Ideal spatial adaptation by wavelet shrinkage", Biometrika,
81(3):425–455, 1994, https://doi.org/10.1093/biomet/81.3.425
[2] Stéphane G. Mallat & Zhifeng Zhang, "Matching pursuits with time-frequency dictionaries", IEEE
Transactions on Signal Processing, 41(12):3397-3415, 1993, https://doi.org/10.1109/78.258082
[3] Shaobing Chen & D. Donoho, “Basis Pursuit”, Proceedings of 1994 28th Asilomar Conference on Signals,
Systems and Computers, pp. 41-44, 1994, https://doi.org/10.1109/ACSSC.1994.471413
[4] Jerome. H. Friedman & John W. Tukey "A Projection Pursuit Algorithm for Exploratory Data Analysis", IEEE
Transactions on Computers. C-23(9):881–890, 1974, https://doi.org/10.1109/T-C.1974.224051
[5] Jon A. Högbom, "Aperture Synthesis with a Non-Regular Distribution of Interferometer Baselines",
Astronomy and Astrophysics Supplement, 15, pages 417-426, 1974 http://adsabs.harvard.edu/full/1974A%26AS...15..417H
[6] Robert Tibshirani, “Regression Shrinkage and Selection Via the Lasso”, Journal of the Royal Statistical
Society: Series B (Methodological), 58:267-288, 1996. https://doi.org/10.1111/j.2517-6161.1996.tb02080.x
[7] Jon F. Claerbout & Francis Muir, "Robust Modeling with Erratic Data," Geophysics 38(5): 826-844, 1973,
https://doi.org/10.1190/1.1440378
[8] Balas K. Natarajan. “Sparse Approximate Solutions to Linear Systems”, SIAM Journal on Computing
24(2):227–234, 1995, https://doi.org/10.1137/S0097539792240406
[9] David L. Donoho & Xiaoming Huo. “Uncertainty principles and ideal atomic decomposition”. ," IEEE
Transactions on Information Theory 47(7):2845–2862, 2001, https://doi.org/10.1109/18.959265
[10] Joel A. Tropp, "Greed is good: algorithmic results for sparse approximation," IEEE Transactions on
Information Theory, 50(10):2231-2242, 2004, https://doi.org/10.1109/TIT.2004.834793
[11] Jean-Jacques Fuchs, « Une approche à l'estimation et l'identification simultanées », Seizième colloque
GRETSI (traitement du signal et des images), pages 1273–1276, 1997, http://hdl.handle.net/2042/12851
[12] Ingrid Daubechies, Michel Defrise & Christine De Mol, “An iterative thresholding algorithm for linear
inverse problems with a sparsity constraint”, Communications on Pure and Applied Mathematics, 57:1413-1457,
2004. https://doi.org/10.1002/cpa.20042
[13] David L. Donoho, "Compressed sensing", IEEE Transactions on Information Theory, 52(4):1289-1306, April
2006, https://doi.org/10.1109/TIT.2006.871582
[14] E. J. Candes, J. Romberg and T. Tao, "Robust uncertainty principles: exact signal reconstruction from
highly incomplete frequency information", IEEE Transactions on Information Theory, 52(2):489-509, Feb. 2006,
https://doi.org/10.1109/TIT.2005.862083
[15] A. C. Gilbert, Y. Kotidis, S. Muthukrishnan and M. Strauss, “Surfing Wavelets on Streams: One-Pass
Summaries for Approximate Aggregate Queries”, VLDB 2001, Proceedings of 27th International Conference on
Very Large Data Bases, Sep 2001, Roma, Italy, pages 79-88, http://www.vldb.org/dblp/db/conf/vldb/vldb2001.html
[16] J. Ables, “Fourier Transform Photography: A New Method for X-Ray Astronomy”, Publications of the
Astronomical Society of Australia, 1(4):172-173, 1968, https://doi.org/10.1017/S1323358000011292
[17] https://laurentjacques.gitlab.io/post/matching-pursuit-before-computer-science/