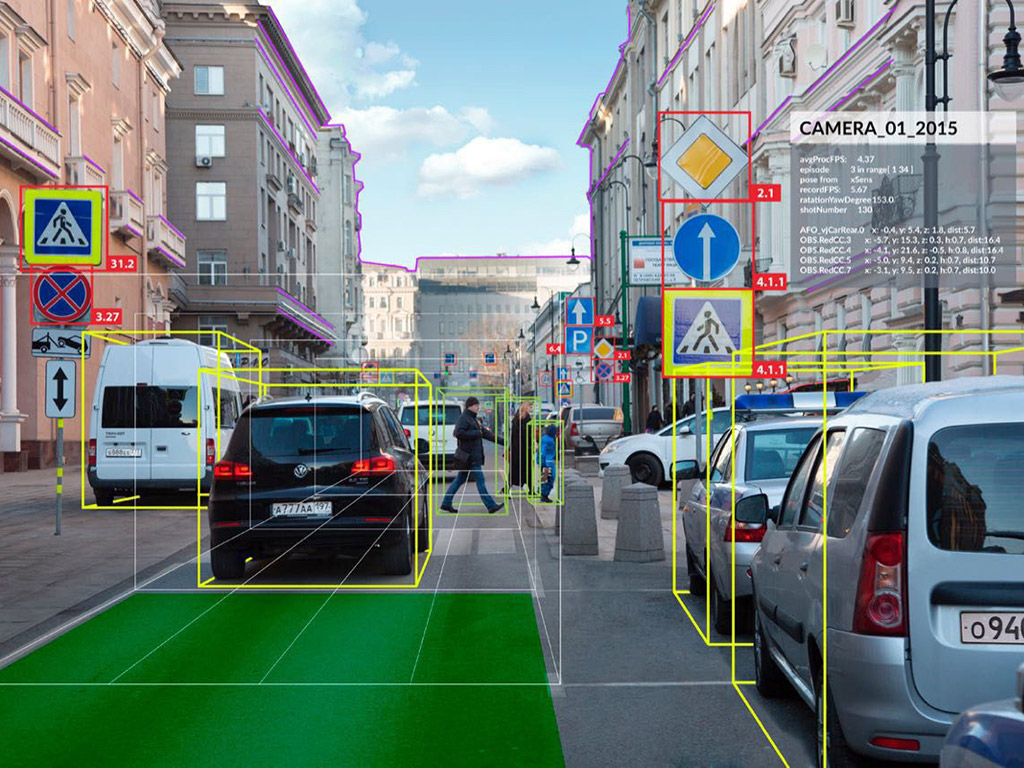
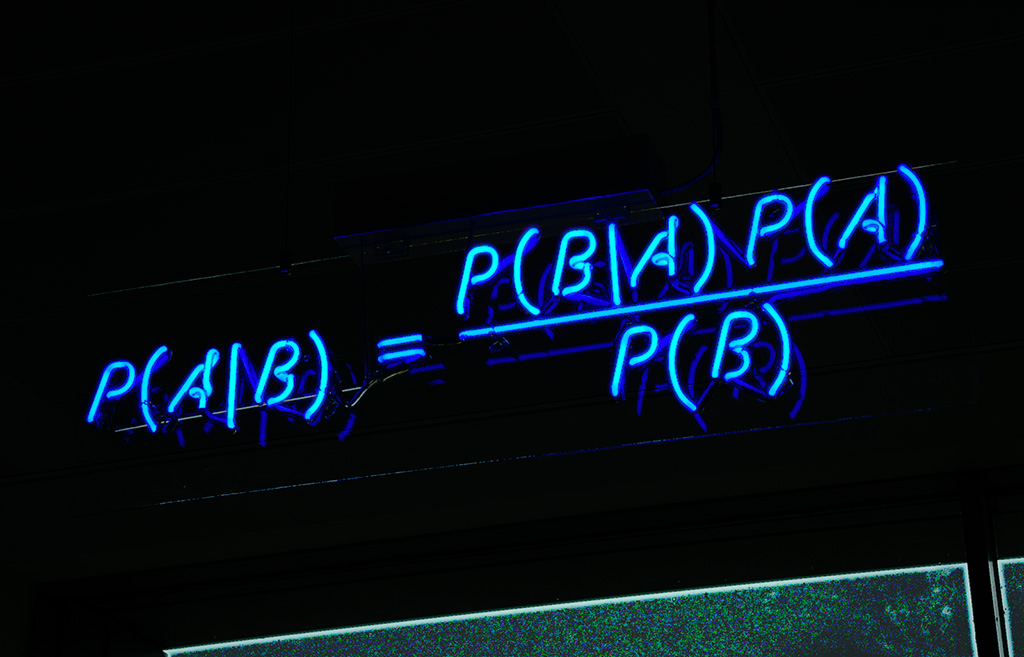L’idée de départ
Le cerveau et le système nerveux constituent des modèles de choix pour le traitement de l’information dont il serait judicieux de s’inspirer.
Les premiers essais de modélisation du Neurone datent de 1943 (Mc Cullogh et Pitts [24]). Quinze ans plus tard, est apparu le Perceptron [23, 26], qui a ouvert la voie aux Réseaux de Neurones Artificiels (RNA). Il s’en suit une période sombre jusqu’à la fin des années 70 où un regain d’intérêt s’est manifesté dans la communauté scientifique, avec, entre autres, les cartes de Kohonen [17], le perceptron multi-couches [25, 27], la machine de Boltzmann, et bien d’autres. Plus récemment, sont apparus les réseaux convolutifs et le « Deep Learning » avec Yann Le Cun [18, 28]. C’est alors l’explosion d’une nouvelle voie de recherche en Intelligence Artificielle, avec des performances impressionnantes dans de multiples domaines d’application (reconnaissance des visages, traduction automatique, robotique autonome, médecine, génome, …).
Dans les années 80, plusieurs disciplines s’y sont intéressées : biologie, informatique (IA), traitement du signal et des images. Mais à cette époque, la biologie et l’informatique ignoraient le traitement du signal, l’informatique et le traitement du signal ignoraient la biologie. Il n’y a que peu de temps que l’on soutient des approches multidisciplinaires (informatique, biologie, psychophysique, mathématique, TSI), ceci dans le cadre des Sciences Cognitives.
Les années 1980 voient aussi le début des premiers congrès internationaux, qui se sont multipliés à travers le monde (ICANN, NEURONIME, IWANN, ESANN…) et qui perdurent encore ainsi que l’apparition de nombreux journaux spécialisés.
Les réseaux de neurones artificiels (RNA)
Ils sont basés sur un modèle hyper-simplifié du neurone biologique, figurant ses propriétés de non linéarités, d’adaptation et d’apprentissage. Au début, ces caractères ont été exploités de manière heuristique, donnant l’impression de « recettes de cuisine ». Puis peu à peu, les mathématiciens et les statisticiens s’y sont intéressés et y ont apporté un cadre théorique.
Les RNA ont développé des applications dans des domaines variés :
- La classification,
- La réduction de dimensions (cartes de Kohonen, Analyse en Composantes Curvilignes, ISOMAP…),
- Le traitement du signal,
- Les Circuits Neuromorphiques (rétines artificielles),
- Le traitement des images basé sur des modèles du Système Visuel (reconnaissance de scènes et de visages, catégorisation de textures…),
- L’Intelligence Artificielle (deep learning)<.
Actuellement on constate un fort développement de l’approche multidisciplinaire et des Sciences Cognitives auxquelles s’intéressent maintenant de nombreuses équipes de recherche dans le monde, de la biologie à la psychophysique en passant par les mathématiques. Récemment sont apparus en Europe et aux Etats Unis des projets pharaoniques - et controversés - de simulation du cerveau comme le Brain Project (un milliard d’Euros …).
Les premiers pas en France
En 1980, fut créée l’association « Neurosciences et Sciences de l’Ingénieur » : NSI.
L’objectif était de faire se rencontrer des ingénieurs, des biologistes, des psychologues et des mathématiciens pour discuter Système Nerveux et Traitement de l’Information et partager leurs travaux et leurs connaissances. La première rencontre ayant réuni 70 chercheurs de toutes disciplines et devant l’enthousiasme général, il fut décidé de la réitérer tous les deux ans sous forme d’un séminaire d’une semaine, avec la tenue de conférences, des exposés par affiche et des démonstrations. L’association a fonctionné ainsi pendant 20 ans. Il est à noter que Yann Le Cun, le « pape » du Deep Learning, a fait partie des premiers participants.
Au début, les réseaux neuronaux ont surtout intéressé les informaticiens, ce n’est que plus tard que sont apparues des applications au traitement du signal [10]. Nous donnerons ici quelques exemples types concernant le traitement des signaux et des images.
L’Analyse en Composantes Indépendantes (ACI ou ICA)
Composante de recherche purement franco-française au début, elle est apparue au Xe colloque GRETSI en 1985 [9], puis en une dizaine d’années, elle s’est étendue au monde entier.
L’idée de départ vient d’un problème de biologie : dans le codage du mouvement par les fibres sensitives neuromusculaires, deux informations sont transmises au système nerveux central. Des fibres dites « statiques » transmettent un mélange d’un signal (plutôt fort) de position et d’un signal (plutôt faible) de vitesse. Des fibres dites « dynamiques » transmettent un mélange d’un signal (plutôt faible) de position et d’un signal (plutôt fort) de vitesse. Mais on ne connaît pas les pourcentages de position et de vitesse dans les deux cas. C’est là qu’a été développée l’idée en remarquant que ces fibres aboutissaient dans le cervelet sur une structure de neurones en inhibition mutuelle. En modélisant cette structure et en la dotant de synapses modifiables de telle sorte que les signaux de sortie soient indépendants, les auteurs on montré que l’un des neurones exhibait le signal de position alors que l’autre exhibait le signal de vitesse.
Ces travaux ouvraient la voie à la formulation du problème de séparation aveugle de sources. Une communauté a émergé autour de cette thématique dans la seconde moitié des années 1980 essentiellement en France et en Finlande. L'algorithme proposé en 1985 était étonnamment robuste mais les explications théoriques de ses propriétés étaient incomplètes. La formalisation mathématique dans le cas de mélanges linéaires instantanés a été effectuée en 1994 par P. Comon, aboutissant au concept « d’Analyse en Composantes Indépendantes » [4, 15]. Voir le texte de Christian Jutten à ce propos.
La réduction de dimensions et l’Analyse en Composantes curvilignes (ACC)
La surveillance ou l’analyse de nombreux systèmes font appel à des mesures multiples (hauts fourneaux, sismique, chimie, analyse d’images, ….), comprenant des dizaines, des centaines ou des milliers de paramètres, occupant des espaces de très grandes dimensions. La première méthode utilisée pour réduire le nombre de dimensions a été l’analyse en composantes principales (ACP). Malheureusement, elle ne convient que rarement, les données occupant souvent une variété de dimension inférieure, mais selon une structure non linéaire. Si l’on ne connaît rien à propos de la structure des données, on va chercher à projeter les données dans un espace de dimension réduite en essayant de préserver au mieux les distances entre les échantillons dans l’espace de départ et leur représentation dans l’espace d’arrivée. Se posent alors plusieurs problèmes.
1. Celui de la « malédiction de la dimension » :
En effet, dans un espace où les données sont aléatoires et de Loi identique, lorsque la dimension \(n\) de l’espace croît, la moyenne des distances euclidiennes entre les échantillons croît comme \(\mu_{\|x\|} = \sqrt{an-b}+\mathcal{O}(1/n)\), alors que la variance tend vers une constante \(\sigma^2_{\|x\|} = b + \mathcal{O}(1/\sqrt{n})\), a et b étant des paramètres qui dépendent uniquement des moments centrés d’ordre 1, 2, 3 et 4 [5]. La figure 1 montre ce phénomène.
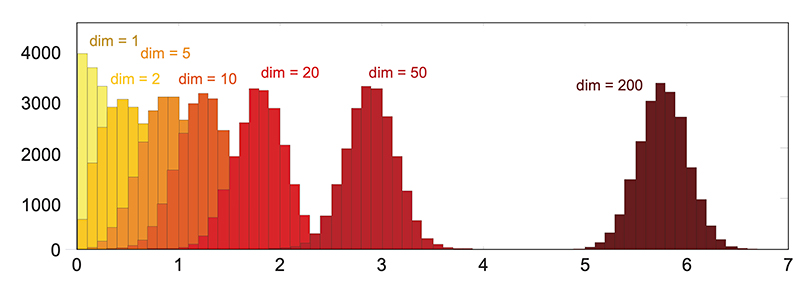
2. Celui de « l’espace vide » :
Le volume d’une coquille, définie (fig. 2) par l’espace entre l’hyper-cube de côté 1 et l’hyper-cube de côté \((1-\epsilon)\), est \(1-(1-\epsilon)^n\). Il tend vers 1 lorsque n augmente : pour \(n=50\) et \(\epsilon=5%\), la coquille représente 92.3% du volume de l’hyper-cube unitaire. L’hyper-cube de côté \(1-(1-\epsilon)^n\) semble donc vide !
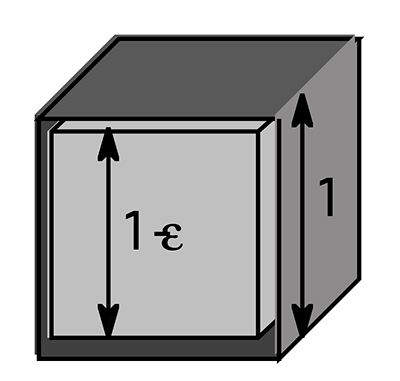
3. Celui de la norme à utiliser :
Le produit scalaire entre un vecteur unitaire sur la diagonale du cube et l’un quelconque des côtés donne un angle qui tend vers 0 lorsque n croît : \(cos(\theta) = 1 / \sqrt(n) \xrightarrow[n \to \infty]{} 0 \) Ce qui ne signifie pas que la diagonale soit orthogonale aux côtés ! Mais simplement que la norme euclidienne n’est pas adaptée. La norme \(L^p\) semble mieux convenir : la figure 3 montre, pour \(p>2\), le lieu des points équidistants de l’origine, ce qui ressemble à l’espace occupé par la coquille précédemment vue. 0n a montré pour un espace initial de dimension \(n\) et une projection à deux dimensions, qu’il faut prendre \(p=1/2+\log(n)/\log(2)\) [14]
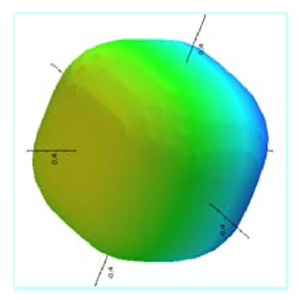
En tenant compte de ces faits, on a développé la méthode « d’Analyse en Composantes curviligne » (ACC) [6] qui permet de réduire la dimension en « dépliant » la variété occupée par les données et en projetant celles-ci sur la variété moyenne (figure 4).
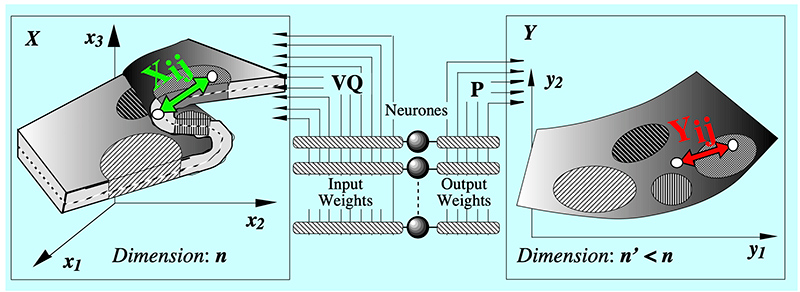
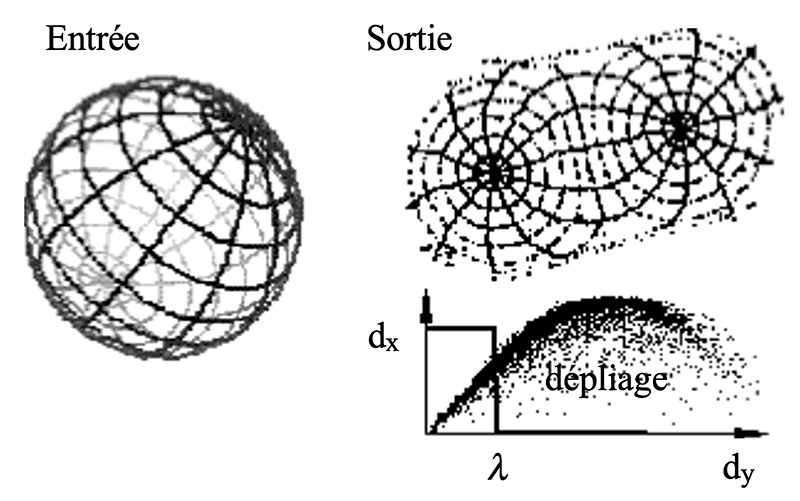
Principe de l’ACC : on quantifie l’espace d’entrée de dimension n et on choisit un espace de représentation de dimension \(n’ < n\). Dans un premier temps, on fait correspondre aux échantillons \(x\) de l’entrée des échantillons \(y\) dans l’espace de sortie, au hasard. Ensuite, on tire deux échantillons d’entrée et éloigne ou on rapproche les échantillons correspondants en sortie de telle sorte que leur distance \(d_y\) se rapproche de celle \(d_x\) des échantillons d’entrée. En fait, on ne fait cela que pour des échantillons de sortie dont la distance \(d_y\) est inférieure à une valeur \(\lambda\) donnée a priori. Puis on itère cette procédure en diminuant progressivement la valeur de \(\lambda\). Le fait de ne pas tenir compte des grandes distances en sortie permet le dépliage de la variété des données d’entrée. Une visualisation du diagramme des distances dans un plan \((dy, dx)\) permet de suivre l’évolution du processus comme l’illustre la figure 5.
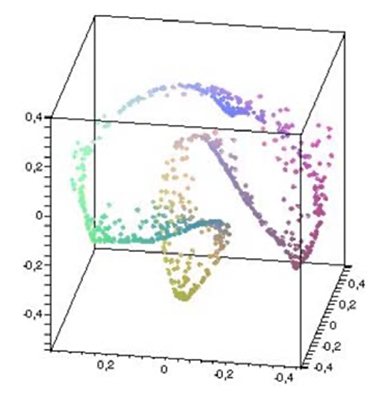
La figure 6 donne un exemple d’application en chimie : une étude de la molécule de Méthylpropylether avec 1000 points de mesures fournit une matrice de 1000 x 1000 distances dans un espace de dimension inconnue. Ces distances sont projetées par ACC sur un espace à 3 dimensions dans lequel les points semblent se répartir sur une bande de Moebius.
L’analyse en composantes curvilignes a trouvé des applications dans des domaines aussi variées que la chimie, la catégorisation d’images, la surveillance de mécanismes (boîte de vitesses, roulements à billes), le routage adaptatif de messages, la reconnaissance de visages, …[14]. Elle a donné lieu à des extensions comme l’analyse en distances curvilignes [19].
Les Circuits Neuromorphiques
C’est en 1989 que l’équipe de Carver Mead [21] a lancé l’idée de réaliser des réseaux de neurones en microcircuits CMOS analogiques. Le modèle des premières couches de cellules de la rétine s’y prête bien car il implique un traitement purement analogique grâce des synapses électriques, donc sans les impulsions que l’on trouve dans les autres structures nerveuses. La décennie qui a suivi a vu se créer une communauté d’une cinquantaine de chercheurs en circuits dits « neuromorphiques » à travers le monde.

Là encore c’est au colloque GRETSI en 1995 qu’a été présentée la première rétine artificielle réalisée en France, à Grenoble [2]. C’était une puce CMOS \(0,5 \mu\) de 64x64 pixels et 250 000 transistors fournissant une image en temps réel et ne consommant quelques microwatts, battant ainsi largement les meilleures performances réalisables en circuits numériques [12].
En s’inspirant de l’architecture de calcul analogique de la rétine, il a été possible d’élaborer un algorithme très performant pour l’estimation du mouvement en temps réel dans une image [29].
Malgré l’intérêt de ces structures de calcul analogique, les recherches se sont réduites, surtout en raison de la difficulté de faire des essais face à la suprématie des circuits numériques : il est très difficile d’insérer un protocole de développement analogique dans une chaîne dédiée à une technologie numérique. En conséquence, ces circuits restent actuellement une curiosité de laboratoire.
Le modèle du Système Visuel
Le système visuel est un modèle de choix pour le traitement des images. La rétine, avec cinq couches de circuits neuronaux derrière les photorécepteurs, réalise un prétraitement sophistiqué des signaux et se projette sur le cortex visuel primaire selon une transformation Log complexe. Cette transformation assure une certaine invariance aux effets de zoom et de rotation ainsi que la possibilité d’estimer l’égo-mouvement. Le cortex visuel primaire procède à une analyse en fréquences spatiales par des filtres passe-bande orientés qui permettent, entre-autre, la catégorisation des images et l’estimation de la perspective monoculaire. Les aires corticales supérieures extraient des informations de haut niveau sur la couleur, le mouvement, l’invariance au zoom et à la rotation et l’association avec d’autres signaux sensoriels [3, 13, 16].
1. La rétine.
Le prétraitement des images trouve un modèle de choix dans la rétine des vertébrés. La rétine se présente d’abord comme un filtre spatio-temporel de type passe-haut à variables non séparables, ce qui lui confère d’intéressantes propriétés de détection des contours et des objets en mouvement. De plus, les photorécepteurs ont une réponse non linéaire (grossièrement logarithmique), ce qui assure une compression d’information, mais aussi adaptative en fonction de l’illumination, ce qui leur confère la possibilité de traiter une grande dynamique de signal d’entrée (six décades), ce qu’illustre la figure 8.

Le traitement de la couleur dans la rétine mérite une attention particulière [11]. Les trois types de photorécepteurs sont disposés au hasard sur une grille approximativement hexagonale centrée. Leur disposition aléatoire permet de réduire drastiquement le phénomène de Moiré. D’autre part, les circuits rétiniens envoient directement au cerveau deux signaux en opposition de couleurs BLEU/JAUNE et ROUGE/VERT, et un signal de LUMINANCE qui sont traités différemment dans des aires corticales spécialisées. Le modèle rétinien de la couleur a permis d’élaborer un algorithme de « démosaïcage » des images en couleur exempt de Moiré et à plus large bande que les techniques classiques [1].
2. L’aire visuelle primaire.
Le cortex visuel primaire est constitué d’un banc de filtres spatiaux de type passe-bande et orientés, selon le modèle Log-Gabor. L’image rétinienne est alors codée en un vecteur de grande dimension (3 à 4 000 composantes). Nous avons exploité ces données dans deux applications : la catégorisation de scènes visuelles et l’estimation de la perspective. Dans ces applications, le banc de filtres comprenait 49 composantes (7 bandes de fréquence et 7 orientations).
Pour la catégorisation de scènes visuelles, on a utilisé la méthode ACC pour « projeter » l’espace à 49 dimensions des sorties des filtres Log-Gabor sur un espace à deux dimensions pour des commodités de visualisation. Les distances dans l’espace d’entrée ont été calculées avec une norme L6 selon l’argumentation définie plus haut [14]. Après convergence, le réseau montre que, dans l’espace de projection, les scènes visuelles (une centaine d’images) sont regroupées par catégories, scènes d’intérieur, plages, montagnes, villes, ainsi que l’illustre la figure 9, ceci de manière automatique et sans supervision [7, 8].

Pour l’estimation de la perspective, on utilise des bancs de filtres Log-Gabor locaux et on estime le gradient spatial des différentes bandes de fréquences (en sommant les énergies en sortie des filtres à travers toutes les orientations). La direction dans laquelle les hautes fréquences glissent donne la ligne de fuite.
Cette méthode convient à tous les types de textures, qu’elles soient régulières, irrégulières ou aléatoires. Elle surpasse les autres techniques classiques d’analyse de textures [20].
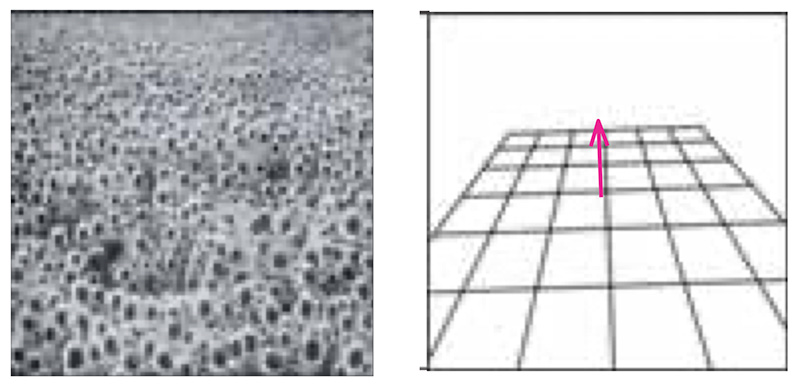
La figure 10 représente l’image d’un champ de tournesols : il s’agit typiquement d’une texture irrégulière et aléatoire. L’algorithme permet d’identifier le plan de la texture, sa normale et les lignes de fuite.
Le « Deep Learning » et l’Intelligence Artificielle.
Depuis quelques années sont apparus les réseaux à apprentissage profond (Deep Learning), c’est-à-dire avec un grand nombre d’étages de traitement. Les premiers étages sont constitués de réseaux de neurones dits « convolutifs », censés mimer les premiers étages du système visuel. Suivent une série d’étages alternant des structures de mutualisations et de convolutions dont les paramètres sont adaptatifs selon des procédures d’apprentissage supervisé (on présente une image, on corrige la réponse du réseau jusqu’à ce qu’il donne une réponse correcte, et on itère un grand nombre de fois). La figure 11 donne un exemple d’une structure à apprentissage profond.
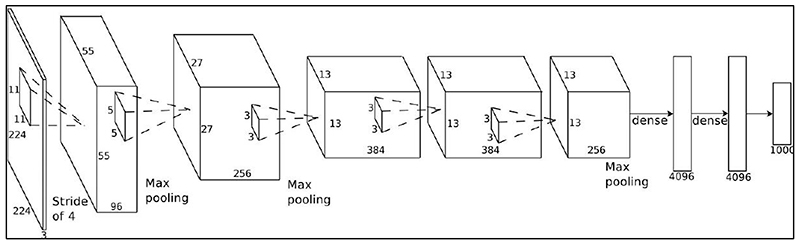
Il existe de nombreux réseaux à apprentissage profond, dont l’architecture comprend de 1 à 10 milliards de connexions, 10 millions à 1 milliard de paramètres, 8 à 20 étages. Les bases de données pour l’apprentissage sont constituées de plusieurs milliers d’exemplaires. Les performances de ces réseaux sont remarquables, par exemple le programme Facebook "DeepFace" (2014) a utilisé une banque de 4 millions d’images dans laquelle il devait reconnaître 4 000 identités. Il a obtenu une précision en reconnaissance de 97.25 %, comparable aux 97.53 % obtenus pour une performance humaine.
On conçoit que la mise en œuvre de tels réseaux nécessite l’utilisation de puissants super calculateurs, très onéreux et accessibles seulement pour un nombre réduit d’utilisateurs. On trouve actuellement des processeurs spécialisés (General-Purpose GPUs) rapides et programmables capables de réaliser jusqu’à 1 Téra opérations par seconde, qui permettront généraliser l’accès aux grandes puissances de calcul. L’apprentissage profond se réclame souvent du modèle du cerveau, ce qui impressionne le grand public et fait les gorges chaudes de certains médias. A ce sujet, il est intéressant de comparer quelques caractéristiques du cerveau et des super calculateurs, telles qu’indiquées dans le tableau suivant (certaines données sont des estimations, mais plausibles).
Le lecteur s’en fera sa propre idée.
| Supercalculateur | Cerveau | |
|---|---|---|
| Nombre d'exemplaires dans le monde | Quelques unités | 7 Milliards |
| Nombre d'opérations par sec | \(200*10^{15}\) | \(\approx 100*10^{15}\) |
| Mémoire | \(10*10^{15} octets\) | \(\approx 10*10^{15} octets\) |
| Surface | \(540 m^2\) | \(0.25 m^2\) |
| Consommation | 15 MW | 20 W |
| Consommation d'eau | \(15 m^3/mm\) | *1 |
| Poids | 340 tonnes | 1.3 kg |
| Nombre d'exemples nécessaires pour reconnaître une église gothique | 1000 | 1 |
| Conscience | Non | Oui |
Références
1. Alleysson, D. Susstrunk S. & Herault J. (2003). Accurate color demosaicing inspired by the Human Visual System, IEEE Image Processing.
2. Bouvier G., Mhani A., Beaudot W., Herault J. (1995), Modélisation VLSI de la rétine des vertébrés, 15ieme Colloque GRETSI, Juan-Les-Pins (France), pp. 1057-1060.
3. Benoit A., Caplier A., Durette B., Herault J. (2010), Using Human Visual System Modeling for Bio-inspired Low Level Image Processing. Computer Vision and Image Understanding 114(7):758-773.
4. Comon P., Jutten C. (1988), Handbook of Blind Source Separation, Independent Component Analysis and Applications, Academic Press.
5. Demartines P. (1992), Analyse de données par réseau de neurones auto-organisés. Thèse de l’INPG, Grenoble.
6. Demartines P., Herault J. (1997). Curvilinear Component Analysis: a Self-Organising Neural Network for Non-Linear Mapping of Data Sets, IEEE Trans. on Neural Networks, 8, 1, 148-154.
7. Guerin-Dugue, A., Oliva A. (2000). Classification of Scene Photographs from Local Orientations Features, Pattern Recognition Letters, vol. 21, pp. 1135-1140.
8. Guyader N. (2004), Scènes visuelles : catégorisation basée sur des modèles de perception, Approches (neuro) computationnelle et psychophysique. Thèse de l’Université Joseph Fourier, Grenoble.
9. Hérault J., Jutten C., Ans B. (1985), Détection de grandeurs primitives dans un message composite par une architecture de calcul neuromimétique en apprentissage non supervisé. GRETSI : Xe Colloque sur le traitement du Signal et ses Applications, Nice.
10. Hérault J., Jutten C. (1994). Réseaux neuronaux et traitement du signal. Hermes, Paris.
11. Hérault J. (1996). A model of colour processing in the retina of vertebrates : from photoreceptors to colour opposition and colour constancy. Neurocomputing.
12. Hérault J. (2001). De la rétine biologique aux circuits neuromorphiques. in "Traité IC2, Les Systemes de Vision", J-M Jolion ed. Hermès.
13. Hérault J. (2010), Vision : Images, Signals and Neural Networks. Models of Neural Processing in Visual Perception. https://doi.org/10.1142/7311. World Scientific.
14. Herault J., Guerin-Dugue A. & Villemain P. (2002). Searching for the embedded manifolds in high-dimensional data, problems and unsolved questions. Tutorial paper, 10th European Symposium on Artificial Neural Networks, Bruges.
15. Jutten C., Hérault J. (1991). Blind Separation of sources. Part. I : An Adaptive algorithm based on neuromimetic architecture. Signal Processing, 24, pp. 1-10.
16. Hérault J. & Durette B. (2007). Models of Visual Perception for Image Processing. Invited paper, International Conference IWANN, June 2007, San Sebastian, Spain.
17. Kohonen T. (1982), Self-Organized Formation of Topologically Correct Feature Maps, Biological Cybernetics, vol. 46, pp. 59–69.
18. Eigen D., Rolfe J., Fergus R. and LeCun Y. (2014), Understanding Deep Architectures using a Recursive Convolutional Network, International Conference on Learning Representations (ICLR2014), CBLS, (OpenReview), (arXiv:1312.1847).
19. Lee J.A., Lendasse A., Verleysen M., (2020), Curvilinear Distance Analysis versus Isomap. ESANN'2002 proceedings - European Symposium on Artificial Neural Networks Bruges, d-side publi., pp. 185-192.
20. Massot C. & Herault J. (2008). Model of Frequency Analysis in the Visual Cortex and the Shape from Texture Problem. International Journal of Computer Vision, 76(2).
21. Mead, Ca. A.; Ismail, Mohammed (1989). Analog VLSI Implementation of Neural Systems. The Kluwer International Series in Engineering and Computer Science. 80. Norwell, MA: Kluwer Academic Publishers.
22. McClelland, J. L.) 318–362 (MIT, Cambridge.
23. Rosenblatt F. (1958), The perceptron: a probabilistic model for information storage and organization in the brain, repris dans J.A. Anderson & E. Rosenfeld (1988), Neurocomputing. Foundations of Research, MIT Press.
24. McCulloch W. and Pitts, W. (1943), A logical calculus of the ideas immanent in nervous activity, Bulletin of Mathematical Biophysics 5: 115-133.
25. Minsky M. L. and Papert S. (1988). Perceptrons : an introduction to computational geometry. MIT Press, expanded edition.
26. Rosenblatt F. (1958). The Perceptron : probabilistic model for information storage and organization in the brain. Psychological Review, 65:386-408.
27. Rumelhart D., Hinton G. & Williams R. (1986), Learning internal representations by error propagation, Parallel Distributed Processing, Vol. 1. D. Rumelhart and J. McClelland Eds. Cambridge: MIT Press, pp. 318-362.
28. Schmidhuber J. (2015), Deep learning in neural networks: An overview, Neural Networks, 61, 85-117.
29. Torralba A. B., Hérault J. (1999). An efficient neuromorphic analog network for motion estimation. IEEE Transactions on Circuits and Systems-I: Special Issue on Bio-Inspired Processors and CNNs for Vision. Vol 46, No. 2.
Notes
1. L’hydratation quotidienne est une nécessité pour le cerveau (attention, concentration).