Le principe des communications numériques est de transmettre des signes en nombre fini à des instants discrets. En pratique on transmet des trames d’une certaine longueur N successivement. Ainsi cette trame peut être vu comme un vecteur, dénoté \(x\), dont les coordonnées sont les signes discrets à transmettre.
En raison du canal de propagation qui la plupart du temps correspond en une multitude d’échos (par exemple, les rebonds des ondes électro-magnétiques sur les obstacles lors d’une communication radio-mobile), le signal reçu \(y\) correspondant à l’émission de la trame \(x\) s’écrit :
$$ y=H.x+w $$
avec \(H\) la matrice représentant ce canal de propagation, et \(w\) le vecteur représentant le bruit ambiant (par exemple, le bruit thermique des récepteurs, les phénomènes non-modélisables par ailleurs et donc considérés comme aléatoires). La matrice \(H\) est supposée connue (il existe des méthodes simples pour l’estimer mais c’est hors du cadre de ce texte).
L’objectif des détecteurs en communications numériques est de trouver la valeur correcte de \(x\) avec pour observation le vecteur \(y\).
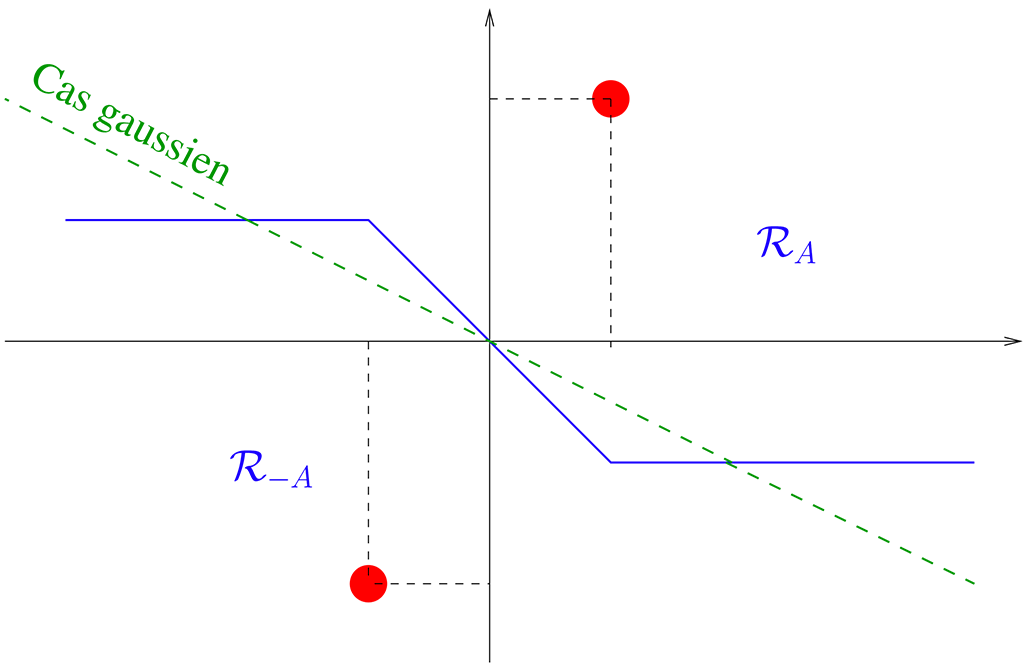
La grande différence entre le traitement du signal pour les communications et de nombreux autres domaines d’application du traitement du signal réside dans le fait que la trame prend un nombre fini de valeurs et donc appartient à un espace discret et donc non-continu et a fortiori non-convexe.
Le cas le plus simple pour résoudre le problème (1) est obtenu quand la matrice \(H\) est diagonale car alors les éléments de la trame ne se mélange pas entre eux. On dit qu’il n’y a pas d’Interférence entre Symboles (IES). Ce cas précis peut être obtenu quand le canal de propagation ne possède pas d’écho et que l’émetteur est conçu de manière adéquate qui a été décrite pour la première fois en 1928 par H. Nyquist dans [1].
Lorsque des échos sont réellement présents (ce qui est la configuration pratique la plus courante), la matrice \(H\) représente en fait un produit de convolution ce qui a conduit à mettre au point des techniques de déconvolution, dites aussi techniques d’égalisation.
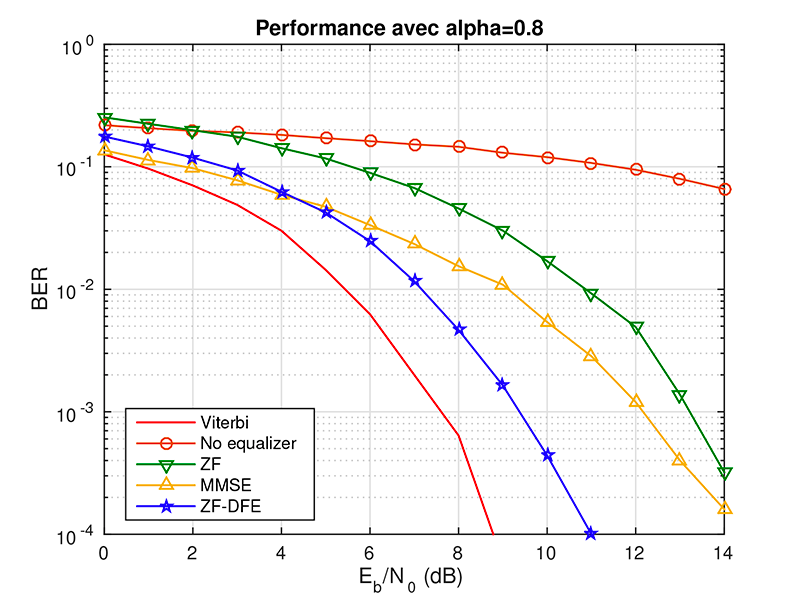
La première idée a été d’appliquer uniquement des traitements linéaires sur le signal reçu \(y\): on peut citer le forçage à zéro en 1964 [2] et 1965 [3] pour sa version adaptative (c’est-à-dire au fil de l’eau et non trame par trame). Cette méthode consiste à inverser la matrice \(H\). Vient ensuite la minimisation de l’erreur quadratique moyenne décrite dans [4] en 1965. Ces techniques sont actuellement peu mises en oeuvre pour gérer l’interférence entre données dues aux rebonds mais sont en vogue pour traiter des interférences entre utilisateurs de cellules différentes ou provenant de plusieurs antennes de transmission (comme dans le massive MIMO - Multiple Input Multiple Output - de la 5G). Une autre approche mélangeant des traitements linéaires et nonlinéaires a été conçue dès 1955 et dénommée « égaliseur à retour de décision » (Decision Feedback Equalizer) qui consiste à utiliser au récepteur les décisions déjà prises sur les données passées pour diminuer l’interférence qu’elles ont créées [5]. Pour ce dernier récepteur, on utilise complètement le fait que les données recherchées x sont à valeurs discrètes. Ce principe, redéveloppé dans [6], est maintenant bien plus utilisé pour la gestion des collisions entre utilisateurs notamment à partir de la 3G.
Néanmoins toutes les approches précédentes ne sont pas optimales au sens de la minimisation des erreurs de détection sur \(x\). La technique optimale dite à maximum de vraisemblance, qui introduit des traitements non-linéaires en lien avec la programmation dynamique et les chaînes de Markov, a été initialement développée en 1967 [7] et utilisée à des fins de déconvolution en 1972 [8]. Elle est néanmoins applicable que dans peu de cas en raison de sa complexité : le cas le plus célèbre est la 2G.
L’équation (1) englobe en fait de nombreuses autres situations que les rebonds d’une communication. Elle peut représenter des systèmes à plusieurs antennes où chaque coordonnée des vecteurs d’entrée et de sortie représente une antenne. Elle peut représenter un système multi-utilisateur où chaque coordonnée correspond à un utilisateur.
Dans le cadre des systèmes MIMO, la matrice \(H\) est souvent de petite taille (sauf très récemment avec le massive MIMO) et n’a pas de structure particulière. Il a été remarqué que ce problème se confond totalement avec un problème de mathématique bien connu qui est la recherche du vecteur le plus proche dans un réseau de points (en anglais, the lattice-based closest vector problem) [9]. Le vecteur \(x\) peut être vu comme un arbre de décision où la n-ème coordonnée correspond à la n-ème couche (les différentes branches sortant de la couche sont les valeurs possibles de cette dite-coordonnée). Donc ce problème se réduit à appliquer une politique judicieuse de lecture de l’arbre de décision. On aboutit par exemple aux premières politiques de R. Fano [10] et F. Jelinek [11]. Une autre idée consiste à réduire les branches possibles [9]. Depuis de très nombreux raffinements et combinaisons ont été développées durant les années 2000.
D’autres liens que l’équation (1) existent entre \(x\) et \(y\), notamment quand les amplificateurs des émetteurs exhibent un phénomène de saturation ou quand les canaux de propagation ont des comportements non-linéaires (par exemple, les fibres optiques à haute puissance d’entrée). On doit alors procéder à de l’égalisation non-linéaire. Le premier travail est de D. Falconer [12] et le plus connu car le plus pratique est de S. Benedetto et E. Biglieri [13].
Actuellement de nombreux travaux existent pour utiliser des réseaux de neurones (et donc le principe de l’intelligence artificielle) comme structure de détecteur afin d’être le plus générique possible.
Références
[1] H. Nyquist, Certain topics in telegraph transmission theory, AIEE Transactions on Communications
Electronics, 1928.
[2] M Rappeport, Automotic equalization of data transmission facility distorsion using transerval
equalizers, IEEE Transactions on Communications Technology, 1964.
[3] R. Lucky, Automatic equalization for digital communications, The Bell System Technical Journal, 1965.
[4] D Tufts, Nyquist’s Problem – the Joint Optimization of Transmitter and Receiver in Pulse Amplitude
Modulation, Proceedings of the IEEE, 1965.
[5] W. Bennett, Synthesis of active network, Symposium on Modern Network Synthesis, 1955.
[6] M. Austin, Equalization of dispersive channels using decision feedback, MIT Res. Lab. Technical Report,
1967.
[7] A. Viterbi, Error bounds for convolutional codes and an asymptotically optimum decoding algorithm, IEEE
Transactions on Information Theory, 1967.
[8] G.D. Forney, Maximum Likelihood sequence estimation of digital sequences in the presence of intersymbol
interference, IEEE Transactions on Information Theory, 1972.
[9] E. Viterbo and J. Boutros, "A universal lattice code decoder for fading channels," IEEE Transactions on
Information Theory, 1997.
[10] F. Jelinek. Fast sequential decoding algorithm using a stack, IBM J.Res. Dev., 1969.
[11] R. Fano. A heuristic discussion of probabilistic decoding, IEEE Transactions on Information Theory,
1963.
[12] D. Falconer, Adaptive equalization of channel nonlinearities in QAM data transmission systems, The Bell
System Technical Journal, 1978.
[13] S. Benedetto, E. Biglieri, Nonlinear equalieation of digital satellite channels, IEEE Journal on
Selected Areas in Communications, 1983.