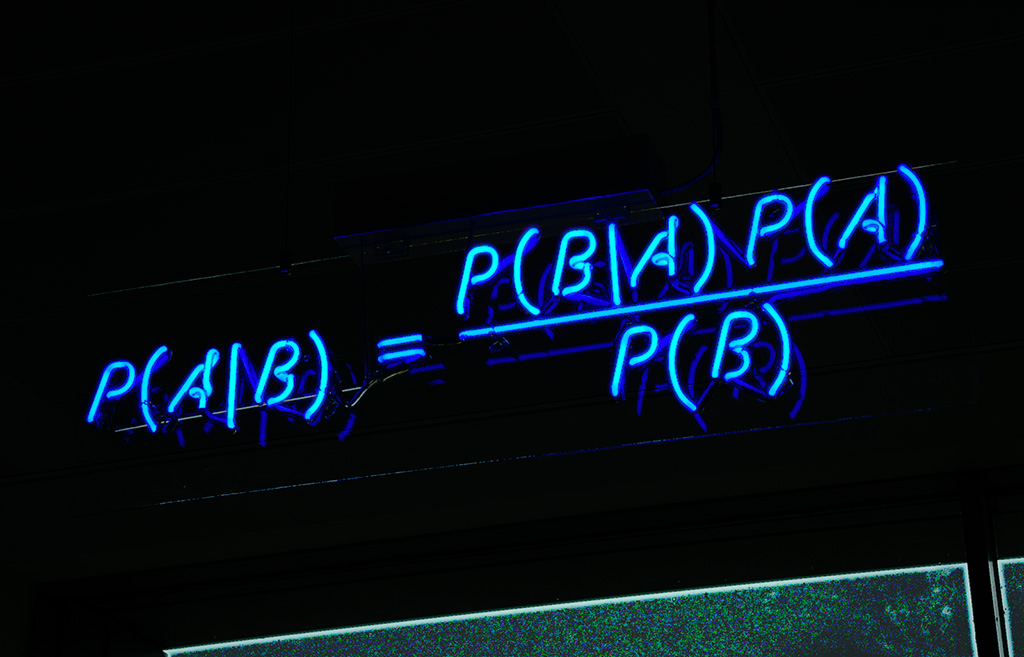L’inférence bayésienne constitue une branche des méthodes statistiques d’estimation.
Elle vise ainsi à déterminer des quantités d'intérêt à partir de mesures capteurs entachées d'erreurs.
Sa particularité est que les paramètres inconnus sont probabilisés : outre l’information apportée par les observations, les méthodes bayésiennes s’appuient donc également sur des connaissances a priori. Les estimateurs sont construits à partir de la loi a posteriori, obtenue en appliquant la règle de Bayes. Ce théorème a été énoncé originellement en 1763 dans un article posthume de Thomas Bayes [1], prêtre presbytérien membre de la Royal Society, puis repris par Pierre Simon de Laplace qui a fortement contribué à formaliser la méthode dite des "probabilités inverses". Le principe est que la distribution de probabilité d’un ensemble de paramètres inconnus \(\theta\) conditionnellement à une collection d'observations \(x\), s’écrit, à une constante de normalisation près, comme le produit de la vraisemblance de \(\theta\) par rapport à \(x\) et de la loi a priori de \(\theta\) :
$$p(\theta | x)=\frac{p(x|\theta)p(\theta)}{p(x)}.$$
Cette loi contient toute l'information disponible sur \(\theta\) et permet d'en calculer un estimé, classiquement en considérant son espérance ou son maximiseur. Le formalisme bayésien offre un cadre unifié et cohérent pour résoudre des problèmes d’inférence et présente l’intérêt de permettre le calcul d’estimateurs optimaux, au sens où ils minimisent une erreur moyenne relativement à l’ensemble des réalisations possibles des paramètres inconnus et des observations. L’analyse bayésienne a essuyé des critiques portant notamment sur le fait de considérer \(\theta\) comme aléatoire, ce qui semble à première vue contredire l’interprétation fréquentiste des probabilités. Cependant, dans le cadre bayésien, la loi a priori a une signification plus subjective au sens où elle traduit le degré d’incertitude sur \(\theta\).
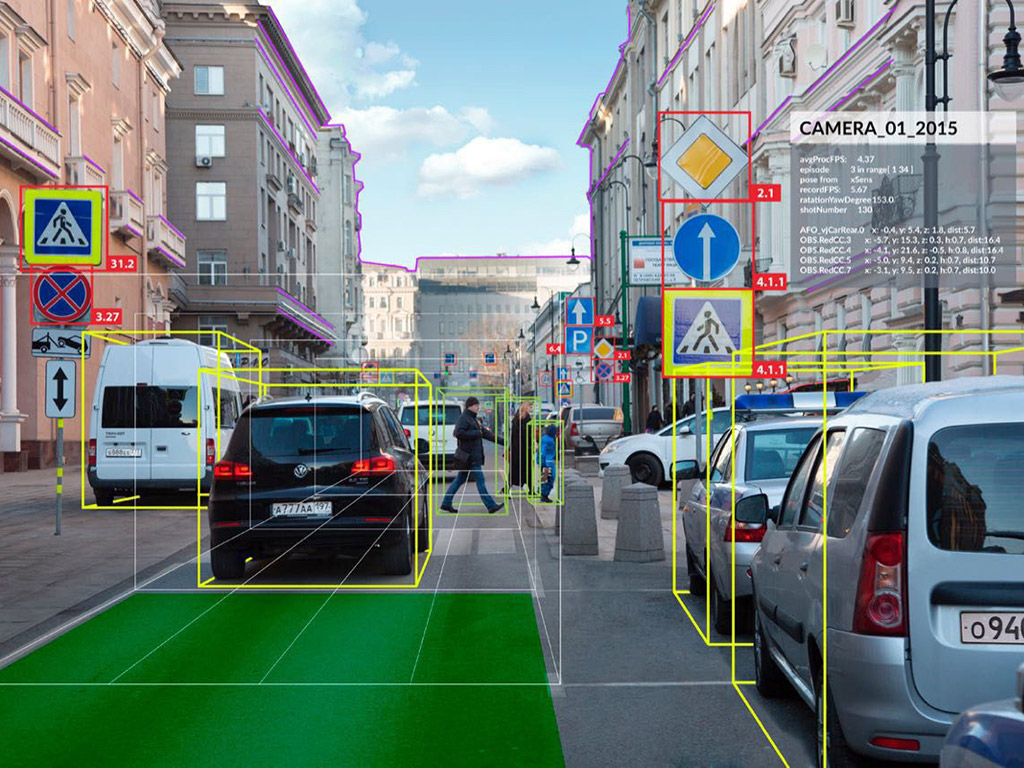
Dans le cas où les paramètres à estimer varient au cours du temps, une formulation récursive de la règle de Bayes a été proposée, également dénommée filtre bayésien optimal. Si les modèles d’évolution et d'observation sont linéaires avec des bruits additifs gaussiens, elle aboutit au filtre de Kalman, utilisé originellement pour estimer des trajectoires de sondes spatiales dans le cadre du programme Appolo de la Nasa en 1960 [2].
Que ce soit dans un contexte statique ou dynamique, une problématique récurrente est que la loi a posteriori peut rarement être calculée analytiquement, aussi l’intérêt pour les méthodes bayésiennes s’est-il renforcé avec le développement des méthodes de Monte Carlo, qui consistent à approcher les lois a posteriori et les estimateurs par échantillonnage. En 1984, l’algorithme de Gibbs est ainsi introduit pour résoudre des problèmes de restauration d’images [3]. Les filtres particulaires, qui s’appliquent à des paramètres variant dans le temps, ont été développés plus récemment au début des années 90 [4].
Actuellement, les approches bayésiennes continuent à susciter beaucoup d’intérêt. Dans la communauté traitement du signal, un des enjeux récents concerne la définition de modèles de probabilité sur des espaces de dimensions infinis. Les méthodes dites bayésiennes non paramétriques permettent ainsi de généraliser l’inférence bayésienne à l’estimation de fonctionnelles et de s’affranchir par exemple de la question du choix de l’ordre dans les modèles de mélange [5]. Enfin, le développement d’algorithmes d’estimation efficaces demeure un sujet d’actualité avec la multiplication des sources de données et donc du nombre d'observations disponibles. Le couplage de méthodes d’optimisation et d’échantillonnage est exploré à cet effet [6].
Références
[1] T. Bayes (1763). Essay towards solving a Problem in the Doctrine of Chances.
[2] R. Kalman (1960). A new approach to linear filtering and prediction problems, ASME - Journal of Basic
Engineering, Vol. 82, pp. 35–45.
[3] S. Geman et D. Geman (1984). Stochastic relaxation, Gibbs distributions and the Bayesian restoration of
images, IEEE Trans. Pattern Anal. Mach. Intell., Vol. 6, pp. 721–741.
[4] N. Gordon, D. Salmond et A.F.M. Smith (1993). Novel approach to non- linear and non-Gaussian Bayesian
state estimation, Proc. Inst. Elect. Eng., F, vol. 140, pp. 107–113.
[5] J. Sethuraman (1994). A constructive definition of Dirichlet priors, Statistica Sinica, Vol. 4, pp.
639–650.
[6] M. Pereyra, P. Schniter, E. Chouzenoux, J.-C. Pesquet, J.-Y. Tourneret, A. Hero et S. McLaughlin (2016),
A survey on stochastic simulation and optimization methods in signal processing, IEEE Sel. Topics in Signal
Processing, Vol. 10, n. 2, pp. 224–241.