L'histoire du Traitement du Signal et des Images

Il faudrait bien plus que quelques pages pour retracer l’histoire de l’analyse temps-fréquence et rendre justice à son développement dans ses multiples ramifications. Quelques rares textes existent en ce sens, comme la monographie [19] qui conduit son propos jusqu’aux lisières de l’analyse en ondelettes, dont l’importance va bien au-delà de son interprétation temps-fréquence. Le choix fait ici est de se concentrer sur les aspects proprement temps-fréquence (à la Wigner, Ville ou Gabor, pour faire court) en s’arrêtant au début de la période contemporaine dont on peut dater le tournant à l’orée des années 80, période qui correspond aussi à l’émergence et la montée en puissance des ondelettes (on se réserve la possibilité de parler spécifiquement des ondelettes dans un autre texte, sachant que d’excellentes perspectives historiques sont d’ores et déjà disponibles [43, 9]). L’analyse temps-fréquence s’appuie par ailleurs sur trois piliers principaux qui relèvent de la physique (mécanique quantique), des mathématiques (analyse harmonique et statistiques) et des sciences de l’information (algorithmes et instrumentation). Il serait vain de chercher à en retracer une généalogie linéaire, la construction progressive du domaine relevant de nombreux emprunts réciproques et allers-retours entre champs disciplinaires naguère distincts : la rédaction de ce court texte s’en accordera.

1. Premières variations autour de Fourier

Qui dit “temps-fréquence” dit “fréquence”, et qui dit “fréquence” dit “Fourier”. S’il ne s’agit pas ici de rendre compte de l’œuvre de Joseph Fourier (1768-1830) — ce que l’on pourra trouver en de multiples endroits et sur de multiples supports, comme par exemple dans une monographie de référence [18], dans un roman graphique [41] ou sur un site dédié au 250ème anniversaire de la naissance du grand homme [62] —, on conviendra en première approximation de dire que l’analyse temps-fréquence telle que nous la connaissons aujourd’hui trouve son origine quelque part dans les années post-Fourier¹, lorsqu’il s’est agi de rendre dépendante du temps l’analyse spectrale, outil central du traitement du signal contemporain et dont l’idée de base apparaît dans le mémoire fondamental de Fourier en 1822 [23].

Si l’on en croit L. Pimonow [46], ce serait Arnold Sommerfeld (1868-1951) qui aurait le premier fait usage de “spectres instantanés”, dans sa thèse de doctorat soutenue à l’Albertus Universität de Könisgsberg en 1890. De façon plus concrète, c’est en fait du côté des instruments de mesure qu’il faut se tourner pour voir apparaître les premières réalisations.

1.1. Instrumentation

En adoptant ce point de vue, la première trace d’une analyse temps-fréquence (qui ne disait pas son nom) remonte sans doute à la construction et la “mise sur le marché” autour de 1862 d’un appareil dû à l’inventeur et acousticien Rudolf Koenig (1832-1901). Il s’agissait d’un ingénieux système fait d’une batterie de résonateurs de Helmholtz de tailles différentes, dont l’excitation était mise en évidence par la modulation d’une “flamme manométrique”, matérialisée par effet stroboscopique grâce à un miroir tournant. Mis en présence d’une onde acoustique, chaque résonateur permettait une réponse sélective en fonction des fréquences constitutives de l’entrée, l’ensemble se comportant comme un banc de filtres. Les sorties de celui-ci dépendant du temps au gré des évolutions de l’entrée, il s’agissait bel et bien d’une analyse temps-fréquence, certes rudimentaire et qualitative, mais effective dans l’utilisation essentiellement pédagogique qui en était faite alors (se reporter à [63] pour une démonstration video). Il est intéressant de noter que nulle référence n’est faite par Koenig à Fourier dans la présentation de ses travaux [64] et que, plus généralement, l’introduction d’une utilisation consciente et dûment créditée des travaux de Fourier pour l’analyse de signaux, en particulier acoustiques, est difficile à dater.

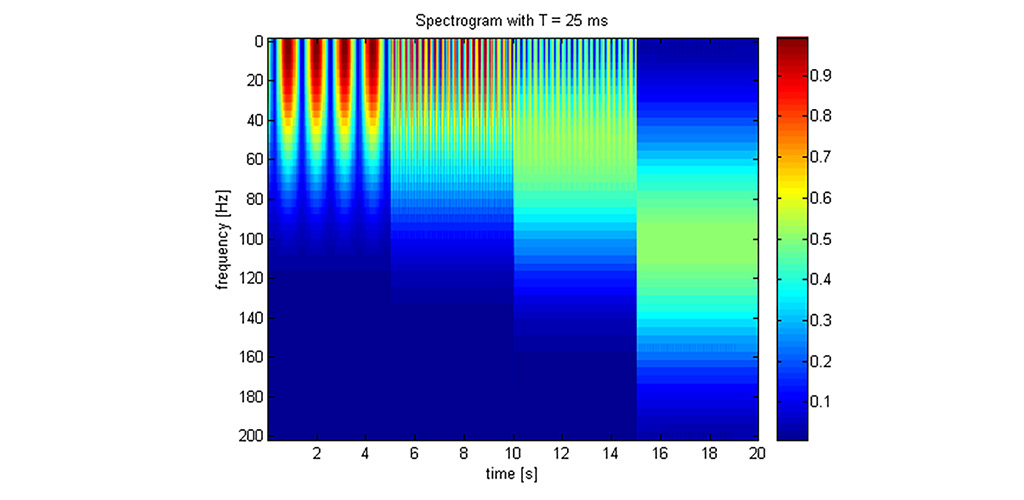
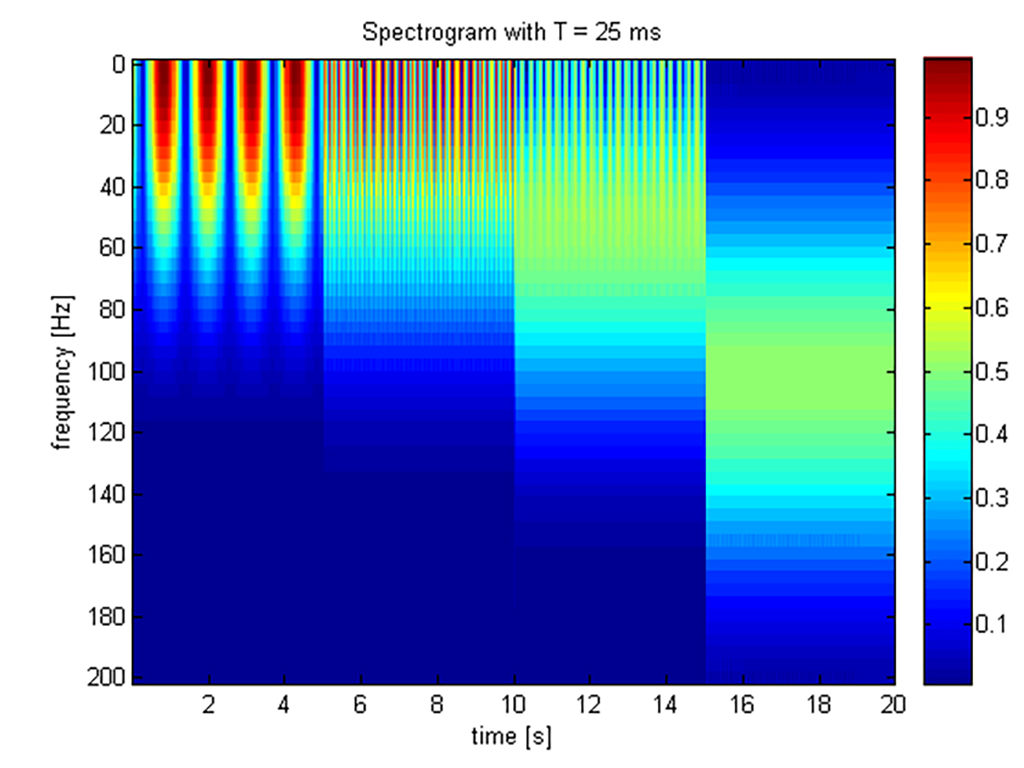
En faisant un saut dans le temps mais en restant dans la veine de l’instrumentation, il est amusant de remarquer que c’est encore à un Koenig (W.) que l’on doit une avancée majeure en 1946 avec la présentation détaillée du sound spectrograph [36], précédée d’une introduction de principe l’année précédente par R.K. Potter [48]. Il s’agit cette fois d’un dispositif électro-mécanique fait d’un cylindre tournant sur la base duquel une piste magnétique encode un signal acoustique. Le cylindre est par ailleurs recouvert de papier électro-sensible dont le noircissement reproduit l’intensité de la sortie d’un filtre passe-bande appliqué au signal. Ce noircissement est opéré grâce à un stylet se déplaçant le long du cylindre de façon verticale et de manière synchrone à la rotation, de telle sorte que la fréquence centrale du filtre varie à chaque tour de rotation. Au terme de l’exploration complète de la bande fréquentielle considérée, le papier est détaché du cylindre et sa mise à plat fournit l’image d’une représentation temps- fréquence appelée “sonagramme” (se reporter à [65] pour une démonstration video). La publication des articles [48] et [36] date de l’immédiat après-guerre mais elle faisait en fait suite à des travaux conduits de manière classifiée aux Bell Labs durant les années 40 [66]. Le passage dans la littérature ouverte et la disponibilité commerciale du matériel correspondant eurent un impact immédiat sur l’exploration et la compréhension d’une multitude de sons naturels (dont la parole) et artificiels [49]. Le sound spectrograph (ou “sonagraphe”) resta en fait d’usage courant dans les laboratoires sous sa forme analogique originelle jusqu’au milieu des années 60, avant d’être remplacé par une forme semblable d’analyseur devenu numérique, bénéficiant des facilités offertes par le développement de l’informatique et la (re-)découverte en 1965 d’un algorithme rapide de calcul pour la transformation de Fourier². L’usage a adopté pour la représentation ainsi obtenue le terme de “spectrogramme”, mettant l’accent sur son obtention comme concaténation de spectres locaux successifs plutôt que comme sorties parallèles de filtres passe-bande. Devenu numérique, le spectrogramme connut ensuite surtout des évolutions algorithmiques relatives au calcul et à l’inversion de transformée de Fourier à court-terme qui le sous-tend [2, 47]. Du fait de l’importance qu’il revêtait en traitement de la parole, il connut aussi des variantes destinées à mieux accorder la représentation spectrale des transformations à celle du système auditif humain, par l’utilisation en particulier de filtres passe-bande à surtension constante [26, 1].

1.2. Gabor

Une façon de concilier les deux points de vue du sonagramme et du spectrogramme est de passer par la vision fournie par Dennis Gabor (1900-1979) en 1946 [24]. En effet, étant donné un signal \(x(t)\) de spectre de Fourier \(X(f)\), la filtrée passe-bande de ce dernier par un filtre passe-bas de gabarit \(H(f)\) s’exprime comme \(X(\xi)H(\xi-f)\) pour une fréquence courante \(\xi\) lorsque le filtre, devenu passe-bande par translation, est centré sur la fréquence \(f\). Il en résulte que le sonagramme associé passe par la mise en parallèle de l’ensemble des formes temporelles de ces filtrées, soit (par transformation de Fourier inverse) :

$$\begin{equation} S_1(t,f) = \int_{-\infty}^{+\infty} X(\xi)H(\xi-f)e^{i2\pi\xi t}d\xi. \end{equation}$$

Du point de vue maintenant du spectrogramme, le calcul repose sur une fenêtre à court- terme \(h(t)\) et met en jeu, pour un temps courant \(\tau\) et chaque instant \(t\) de centrage de la fenêtre, le segment \(x(\tau)h(\tau - t)\) dont est évalué le spectre de Fourier selon :

$$\begin{equation} S_2(t,f) = \int_{-\infty}^{+\infty} x(\tau)h(\tau-t)e^{-i2\pi f \tau}d\tau. \end{equation}$$

À condition que \(h(t)\) et \(H(f)\) soient transformées de Fourier l’une de l’autre, on a l’égalité “\(S1 = S2\)” à des termes de phase près, conduisant à l’identité des sonagramme et spectrogramme correspondants. De plus, les deux expressions (1) et (2) peuvent se mettre sous une forme semblable

$$\begin{equation} G(t,f) = \langle x,{\bf T}_{tf}h\rangle \end{equation}$$

moyennant l’introduction d’un opérateur convenable \({\bf T}_{tf}\) de translation en temps et en fréquence.

C’est précisément cette approche qui a été suivie par D. Gabor [24] en y ajoutant un ingrédient supplémentaire qui est celui de la discrétisation. En effet, les différents produits scalaires (3) peuvent être vus comme des projections résultant en des “grains d’information” prélevés sur le signal au voisinage du point temps-fréquence d’intérêt \((t,f)\). Le voisinage en question est naturellement défini par la largeur en temps \(\Delta t\) de la fenêtre à court-terme \(h(t)\) et la largeur en fréquence \(\Delta f\) du filtre \(H(f)\). Comme le montre D. Gabor dans son article fondateur, ces deux quantités sont couplées par l’inégalité

$$\begin{equation} \Delta t\,\Delta f \geq \frac{1}{4\pi}, \end{equation}$$

exprimant que la localisation temporelle ne peut se faire qu’au détriment de la localisation fréquentielle, et vice-versa. L’intuition est alors (i) de maximiser la localisation en utilisant pour fenêtre/filtre la fonction minimisant l’inégalité (4), qui se trouve être la gaussienne, et (ii) en prélevant les grains d’information sur une grille dont le maillage (rectangulaire) est asservi à l’encombrement temps-fréquence des fonctions analysantes \({\bf T}_{tf}h\).

La proposition initiale de Gabor était de choisir une grille de discrétisation à densité minimale (ni perte d’information ni redondance) de telle sorte que l’ensemble des fonctions analysantes forme une base orthonormée, mais il apparut rapidement que ce choix, associé à celui des gaussiennes comme fonctions élémentaires, posait des problèmes d’instabilités numériques. L’usage s’en accorda avec l’adoption de décompositions redondantes [29] ou de fonctions d’analyse différentes de la gaussienne [44, 39]. La question plus fondamentale d’obtenir une base “à la Gabor” resta cependant quelque peu en suspens jusqu’en 1980, lorsque Martin J. Bastiaans explicita le calcul des coefficients de Gabor par une technique de base réciproque, mettant en évidence le mauvais conditionnement de la solution lorsqu’on s’approche du cas critique [5]. Le coup de grâce fut porté l’année suivante par Roger Balian [3] qui montra qu’à un maillage rectangulaire à densité minimum ne peut être associée aucune base construite sur des fonctions bien localisées en temps et en fréquence³.

Base orthonormée ou pas, on peut considérer les “gaborettes” élémentaires \({\bf T}_{tf}h\) comme des “atomes” temps-fréquence ou encore des “quanta” d’information, ce que Gabor appelle des “logons”. Gabor était physicien (lauréat du Prix Nobel de Physique en 1971 pour l’invention de l’holographie) et l’analogie qu’il fait avec la physique n’est ni fortuite ni gratuite, ce qui nous amène à faire un détour par la mécanique quantique, quitte à remonter le temps avant de rejoindre le fil des développements que l’analyse temps-fréquence a connus dans la deuxième moitié du XXème siècle.

2. Un détour par la mécanique quantique

Les variables de temps et de fréquence ont le statut particulier de porter des représentations qui sont en relation de dualité par transformation de Fourier : on dit qu’elles sont “canoniquement conjuguées”. Toute paire d’autres variables semblablement liées offre un cadre de représentation parallèle, tant en possibilités qu’en limitations, à celui rencontré dans le cas temps-fréquence. Il en est ainsi en mécanique pour les variables de position \(q\) et d’impulsion \(p\), utilisées comme coordonnées d’un “espace des phases” dans lequel se déploie la dynamique d’un système (exemple de l’oscillateur harmonique dont l’hamiltonien s’écrit \(H = p2 + q2\) en coordonnées réduites). Théorie du signal et mécanique (quantique) partagent ainsi un cadre mathématique formel de représentation, permettant des allers-retours entre les deux domaines.

2.1. Incertitude

Tout comme l’analyse temps-fréquence d’un signal se heurte à l’impossibilité d’une localisation conjointe parfaite d’après (4), décrire un système mécanique conjointement en position et en impulsion trouve aussi une limite dont l’importance prend tout son sens lorsqu’on aborde le monde quantique. On attache usuellement à cette limite le nom de Werner Heisenberg (1901-1976, Prix Nobel de Physique en 1932) qui, le premier, formula en 1927 [28] un “principe d’incertitude (ou d’indétermination)” du type

$$\begin{equation} \Delta p\,\Delta q \geq \frac{\hbar}{2}, \end{equation}$$

sur la base d’arguments essentiellement phénoménologiques. Hermann Weyl (1885- 1955) replaça peu après cette question dans le cadre mathématique général de l’analyse de Fourier [57], justifiant à la fois la limite (5) posée par Heisenberg l’année précédente et l’inégalité (4) que Gabor redémontrera presque vingt ans plus tard.

2.2. Distributions

Ce faisant, il apparut que la représentation conjointe “position-impulsion” d’un état quantique posait des problèmes nouveaux et appelait des solutions spécifiques. En mécanique quantique, une mesure physique est liée à la valeur moyenne d’un opérateur \(G\) prise sur l’état d’un système via sa fonction d’onde \(\psi\). Afin de procéder de façon quasi-classique, Eugene P. Wigner (1902-1995, Prix Nobel de Physique en 1963) proposa en 1932 [59] de représenter l’état par une “distribution de quasi-probabilité” \(P (q, p)\), fonction conjointe de la position et de l’impulsion, de telle sorte que le même résultat de mesure soit obtenu par une simple moyenne prise sur la fonction classique \(G(q, p)\) décrivant la quantité physique d’intérêt, sans passage donc par un opérateur associé ⁴. En d’autres termes, il s’agissait d’assurer l’égalité :

$$\begin{equation} \langle \psi | {\bf G} | \psi\rangle = \int\!\!\int_{-\infty}^{+\infty} G(q,p) \,P(q,p) \,dq\, dp. \end{equation} $$

Sur la base d’un argument de simplicité (et de bonnes propriétés marginales), Wigner proposa pour cela la forme suivante, aujourd’hui connue sous le nom de “distribution de Wigner” :

$$\begin{equation} P(q,p) = \frac{1}{\pi\hbar}\int_{-\infty}^{+\infty} \psi(q+y)\psi^*(q-y)e^{i2\pi py/\hbar} dy. \end{equation} $$

Cette proposition était néanmoins purement ad hoc⁵ et plusieurs difficultés lui sont attachées. La plus visible est que la “quasi-distribution” (7) peut prendre des valeurs négatives, lui interdisant de fait d’être interprétée comme une véritable densité de probabilité. Plus fondamentalement, l’association d’un opérateur à une grandeur classique n’est pas unique du fait de la non-commutativité des opérateurs élémentaires associés aux variables de position et d’impulsion. Ceci nécessite le choix d’une “règle de correspondance” dont l’arbitraire rejaillit nécessairement sur la fonction conjointe.

Sans entrer dans les détails, il apparaît que la distribution de Wigner est naturellement liée au choix de la correspondance dite “de Weyl” [56], mais d’autres choix sont envisageables. Les années qui suivirent l’article de Wigner virent ainsi apparaître d’autres formes possibles de quasi-distributions liées, implicitement ou explicitement, à d’autres règles de correspondance, sans qu’aucune cependant marquât d’avantage déterminant sur les autres. Il fallut attendre 1966 pour observer une avancée majeure, qui permit en quelque sorte de clore une partie du débat. C’est en effet cette année-là que Leon Cohen publia un article [13] montrant que toutes les formes proposées jusqu’alors (et, plus généralement, une infinité d’autres possibles) s’inscrivaient dans le cadre d’une formulation générale dont elles n’étaient chacune qu’un cas particulier, moyennant le choix convenable d’une fonction de paramétrisation directement liée au choix d’une règle de correspondance (cette dernière question faisant ensuite l’objet de considérations plus systématiques [54]).

On se contentera à ce point de décrire la formulation proposée par Cohen de la façon suivante : si la distribution de Wigner (7) est formellement interprétée comme une distribution de probabilité, sa double transformée de Fourier acquiert le statut d’une fonction caractéristique. Il suffit alors de multiplier cette fonction caractéristique par une fonction de pondération (raisonnablement) arbitraire pour obtenir, après double transformée de Fourier inverse, l’ensemble de la “classe de Cohen”. Dans son article original, Cohen a essentiellement trouvé comment inscrire dans un cadre commun différents objets proposés dans la littérature et a ouvert la voie à en construire de nouveaux. La démarche était cependant d’observation mais il a pu être montré plus tard qu’une construction axiomatique de la classe de Cohen était possible sur la base de contraintes de covariance [37].

2.3. Positivité

Les approches “à la Wigner” reçurent des marques d’intérêt mais connurent aussi une difficulté d’acceptation dont une des raisons principales a longtemps été l’existence de valeurs négatives (voire complexes) dans les distributions considérées. Si beaucoup serait à dire sur l’interprétation de ces distributions, et s’il a pu être prouvé par exemple que la positivité était l’exception pour la distribution de Wigner (R.L. Hudson a ainsi montré dans [33] que ce n’était le cas que pour les gaussiennes), plusieurs tentatives ont été faites pour garantir la positivité en toutes circonstances. Une façon naturelle de faire est de “régulariser” la distribution de Wigner par lissage, ce qui conduit formellement à une distribution ayant la forme d’un spectrogramme ! Il en est ainsi pour la distribution dite “de Husimi” [34], qui s’appuie sur une fonction d’onde auxiliaire gaussienne jouant le rôle d’une fenêtre d’observation. Une approche de même nature, quoique plus générale dans le choix de la fonction auxiliaire et dans son interprétation, sera encore proposée au début des années 70 [38].

Pour rester dans le cadre de la positivité, un résultat majeur a finalement été fourni par Eugene P. Wigner lui-même qui, en 1971 — soit une quarantaine d’années après la publication de son article de base —, prouva un théorème d’exclusion selon lequel une distribution conjointe ne peut à la fois être bilinéaire, avoir des distributions marginales correctes et être partout non-négative [60]. Ainsi, la distribution de Wigner est bilinéaire et possède des marginales correctes mais elle prend aussi des valeurs négatives de façon générique; à l’inverse, une régularisée “à la spectrogramme” est bilinéaire et partout non-négative mais ses marginales sont biaisées. La seule issue est de relâcher la contrainte de bilinéarité, ce qui a été envisagé [17], quoiqu’au prix de difficultés d’interprétation qui en ont limité l’usage.

2.4. Décompositions

Le détour que l’on a emprunté en direction de la mécanique quantique était au départ partiellement motivé par l’incursion du physicien Gabor dans le champ de la théorie de la communication, mais la remontée dans le temps jusqu’à Wigner nous a conduits dans un monde de représentations (au moins) quadratiques, pouvant sembler moins naturel que les décompositions linéaires proposées dans [24]. De telles décompositions/représentations linéaires ont néanmoins fait leur chemin dans un second temps, avec l’introduction au début des années 60 du concept d’“état cohérent” par Roy J. Glauber (co-lauréat pour cela le Prix Nobel de Physique en 2005) [27]. Il y a en fait une filiation directe entre les paquets d’ondes gaussiens (les “logons” de Gabor) et les états cohérents de Glauber, ce qui a donné lieu dans les années 70 à une abondante littérature en physique mathématique et à des applications nombreuses, en particulier en optique quantique [35].

2.5. Passerelles

Pour conclure cette partie, on peut dire que la littérature de mécanique quantique a offert un certain nombre de considérations théoriques sur lesquelles les approches temps- fréquence peuvent s’appuyer mais il faut reconnaître que peu de physiciens ont investi de façon explicite le domaine du signal. Une exception notable est fournie par Leon Cohen, qui a introduit en théorie du signal la méthode opératorielle de la fonction caractéristique [15] et a abordé de façon générale l’analyse temps-fréquence en se basant pour part sur ce que le formalisme de la mécanique quantique pouvait offrir [14]. Réciproquement, peu nombreux furent les chercheurs de la communauté du signal à investir le champ de l’analyse temps-fréquence par le prisme du formalisme opératoriel de la mécanique quantique. Georges Bonnet fut parmi ceux-ci [8], suivi par Bernard Escudié et Jean Gréa [20] : on trouvera une synthèse et des développements en ce sens dans [21]. En revanche, les nombreux travaux temps-fréquence conduits de manière interne à la communauté du traitement du signal ont reçu peu ou pas d’écho en physique. En anticipant sur ce qu’on dira des évolutions proprement temps-fréquence, il est intéressant à ce propos de constater que le cheminement conceptuel en mécanique quantique et en signal a suivi en quelque sorte des voies inverses, entre un objet purement théorique (la distribution de Wigner) et un objet pragmatique (le “spectrogramme”), chacun étant considéré comme naturel et premier dans son domaine, et résultat d’une élaboration dans l’autre.

En situant l’analyse temps-fréquence dans une perspective “post-Fourier”, il est un autre type de passerelles qu’il faut mentionner : celles qui la rattachent à l’analyse harmonique. Pour rester dans le cadre de cette partie plus spécifiquement centrée sur la mécanique quantique, on notera que l’approche opératorielle est en lien direct avec le calcul pseudo-différentiel [32]. Comme on l’a évoqué précédemment, il n’y a pas de règle unique permettant de mettre en correspondance une fonction définie sur l’espace des phases et un opérateur. Selon la terminologie consacrée dans le cadre du calcul pseudo-différentiel, la fonction en question est le “symbole” de l’opérateur, et elle est en relation de dualité de Fourier partielle avec le noyau de ce même opérateur. Ainsi, la distribution de Wigner d’un état donné peut être vue comme le symbole de Weyl de l’opérateur de projection orthogonale sur l’état. D’autres choix de symboles que celui de Weyl sont néanmoins possibles, conduisant à d’autres formes de distributions. On pourra se reporter à [22] pour un traitement mathématique précis de telles questions d’analyse harmonique sur l’espace des phases.

3. Ville et après

Revenons au temps-fréquence proprement dit et reprenons l’histoire à la fin des années 40, en nous plaçant plus précisément en 1948. Cette année-là est en fait une annus mirabilis : elle voit naître à la fois la théorie de l’information de Claude E. Shannon (1916-2001) [53] et la cybernétique de Norbert Wiener (1894-1964) [58], et elle suit de quelques mois l’invention du transistor par John Bardeen, William Shockley et Walter Brattain (ce qui leur vaudra d’être co-lauréats du Prix Nobel de Physique en 1956) et la mise en service de l’ENIAC, premier ordinateur programmable et entièrement électronique. Il est remarquable de constater la concomitance de ces avancées dans un périmètre réduit de la Côte Est des États-Unis (Bell Labs, MIT, université du Maryland) et la mise en place de façon quasiment simultanée de tous les ingrédients — théoriques, algorithmiques et matériels — qui seront au cœur de l’ère de l’information qui est aujourd'hui la nôtre.

3.1. Spectre instantané

Aux contributions majeures qui viennent d’être citées s’ajoute celle, plus confidentielle, de Jean Ville [55], dans laquelle l’auteur introduit la définition devenue classique de fréquence instantanée, sur la base du concept de signal analytique qui était déjà en germe chez Gabor [24]. Il y définit également un “spectre instantané” destiné à répartir l’énergie d’un signal dans le plan temps-fréquence sur la base d’une analogie probabiliste. Son point de départ est de construire une “forme acceptable de fonction caractéristique” du temps et de la fréquence, qu’il propose d’écrire :

$$\begin{equation} A(\xi,\tau) = \int_{-\infty}^{+\infty} x\left(s+\frac{\tau}{2}\right)x^*\left(s-\frac{\tau}{2}\right)e^{i2\pi \xi s}ds, \end{equation}$$

et d’en déduire la “distribution de probabilité” associée par double transformée de Fourier. La grandeur qui en résulte prend la forme

$$\begin{equation} P(t,f) = \int_{-\infty}^{+\infty} x\left(t+\frac{\tau}{2}\right)x^*\left(t-\frac{\tau}{2}\right)e^{-i2\pi f\tau}d\tau, \end{equation}$$

qui n’est autre, mutatis mutandis, que celle de la distribution de Wigner (7). Nulle référence n’étant faite par Ville au travail de Wigner, il semble que celui-ci n’en avait pas connaissance et, du fait de l’indépendance supposée des deux définitions, il est parfois fait référence à la distribution “de Wigner-Ville”.

3.2. Ambiguïté

Revenant à l’origine de la distribution (9) au sens de Ville, on pourra se reporter à [55] pour comprendre en quoi (8) est une “forme acceptable de fonction caractéristique”, mais cette expression admet une interprétation physique beaucoup plus tangible. En effet, en raisonnant en termes de produit scalaire de L2(R), il est facile de se convaincre que (8) mesure un degré de ressemblance entre un signal et une version de celui-ci décalée en temps et en fréquence, tout comme la représentation de Gabor (3) mesurait un degré de ressemblance entre un signal et une batterie d’atomes de référence. Ceci ra- mène naturellement à la situation communément observée en radar/sonar, dans laquelle l’écho d’un signal émis est une version retardée (décalage en temps) et dopplérisée (décalage en fréquence). Il s’ensuit que l’expression (8) est directement liée à la sortie du récepteur optimal (filtre adapté) qui opère par corrélation signal-écho : on parle alors de “fonction d’ambiguïté”. Cette remarque d’interprétation ouvre une fenêtre sur tout un pan de littérature consacrée aux fonctions d’ambiguïté à partir du milieu des années 50 à la suite des travaux pionniers de P.M. Woodward [61] et jusque vers la fin des années 60 [52]. Il faut noter que, dans cette interprétation, (8) n’est aussi qu’une “forme acceptable de fonction d’ambiguïté”, essentiellement vis-à-vis de la symétrisation des opérateurs de décalage. D’autres symétrisations conduiraient à d’autres définitions, différant essentiellement par la présence d’un facteur de phase préalable à la transformation de Fourier inverse, et rejoignant ce faisant le giron de la classe de Cohen comme évoqué précédemment.

3.3. Variations

Tout comme en mécanique quantique, le domaine de l’analyse temps-fréquence vit fleurir un certain nombre de propositions alternatives dans les années qui suivirent l’article de Ville de 1948, mais en ordre dispersé et sans nécessairement faire usage de références croisées explicites. On vit ainsi apparaître en 1952 une forme causale de spectrogramme, la “distribution de Page” [45], sur la base de laquelle André Blanc-Lapierre et Bernard Picinbono proposèrent en 1955 des variations et des premières tentatives d’unification [6]. Ils suggérèrent ainsi une version anti-causale de la distribution de Page, qui allait être introduite ultérieurement de façon indépendante en 1967 et devenir la “distribution de Levin” [40]. Ils montrèrent en outre que la demi-somme des distributions de Page et de Levin s’identifiait à la partie réelle de la quantité :

$$\begin{equation} R(t,f) = x(t) X^*(f) e^{-i2\pi ft}, \end{equation}$$

quantité introduite elle aussi ultérieurement en 1968 et connue depuis sous le nom de “distribution de Rihaczek” [51]. On notera que l’introduction de la distribution de Rihaczek dans [51] reposait sur un argument tout autre : elle apparaissait comme limite de l’énergie d’interaction entre un segment de signal prélevé sur un intervalle temporel \(\delta t\) autour de \(t\) et une filtrée passe-bande de ce même signal dans un intervalle fréquentiel de largeur \(\delta f\) autour de \(f\) , lorsque \(\delta t \rightarrow 0\) et \(\delta f \rightarrow 0\). Il est à noter que, non seulement cette distribution n’est pas non-négative, mais qu’elle est à valeurs complexes.

Tout comme en mécanique quantique, l’ensemble de ces propositions trouve son unification dans le cadre de la “classe de Cohen” [13] qui, dans le contexte temps-fréquence, prend la forme :

$$\begin{equation} C(t,f) = \int\!\!\int_{-\infty}^{+\infty} \varphi (\xi,\tau)\,A(\xi,\tau)\,e^{-i2\pi(\xi t + \tau f)}\,d\xi\,d\tau, \end{equation}$$

expression dans laquelle \(\varphi (\xi,\tau)\) est une fonction de paramétrisation dont les propriétés fixent celles de la distribution associée [21, 14].

3.4. D’autres voies encore

Même si allusion a été faite aux décompositions linéaires et si l’accent a été mis prioritairement sur les approches quadratiques, il s’agissait dans les deux cas de prendre pour objet d’analyse des signaux supposés déterministes. Il existe cependant tout un pan de l’analyse spectrale qui se réfère à des signaux ou processus aléatoires, l’enjeu n’étant plus de rendre dépendante du temps la transformée de Fourier \(X(f )\) ou la densité spectrale d’énergie \(|X(f)|^2\) qui lui est associée, mais bien davantage la notion de densité spectrale de puissance qui, dans le cas stationnaire, résulte de la relation de Wiener-Khintchine-Bochner :

$$\begin{equation} \Gamma(f) = \int_{-\infty}^{+\infty} \gamma(\tau)\,e^{-i2\pi f\tau}\,d\tau, \end{equation}$$

où \(\gamma(\tau) = {\mathbb E}\{x(t)x^*(t-\tau)\}\) représente la fonction de corrélation du processus, considéré d’un point de vue de moyenne d’ensemble. Plusieurs travaux se sont attachés à cette question, mais ils sont plutôt à trouver dans la littérature de statistique ou de séries temporelles.

L’approche la plus immédiate est bien sûr d’appliquer les méthodes du cas certain aux réalisations d’un processus aléatoire et, sous réserve d’existence, d’en prendre la moyenne d’ensemble : \(P(t,f) \rightarrow {\mathbb E}\{P(t,f)\}\). De manière plus fondamentale, une possibilité est de partir de la représentation spectrale :

$$\begin{equation} x(t) = \int_{-\infty}^{+\infty} e^{i2\pi ft}\,dX(f) \end{equation}$$

qui est doublement orthogonale dans le cas stationnaire (vis-à-vis tant des exponentielles complexes que des accroissements spectraux) et de relâcher l’une ou l’autre de ces orthogonalités.

S’il en est ainsi pour les accroissements spectraux, on entre dans le cadre de l’harmonisabilité au sens de Cramér et la définition d’un “spectre dépendant du temps” devient possible en considérant la fonction de covariance non stationnaire à deux dates \(r(t_1,t_2) = {\mathbb E}\{x(t_1)x^*(t_2)\}\), dont on prend la transformée de Fourier partielle relativement à une variable considérée comme décalage temporel \(\tau\) autour d’un instant courant \(t\) : c’est ainsi que l’on peut construire un “spectre de Wigner-Ville” par symétrisation de la fonction de corrélation selon \(r(t_1,t_2) \equiv r(t+\tau/2,t-\tau/2)\), approche dans laquelle la définition du spectre se double d’une classe d’estimateurs fournie par la classe de Cohen [42].

Si l’on souhaite maintenant privilégier la double orthogonalité, il faut remplacer les exponentielles complexes par les fonctions \(\psi(t,f)\) qui sont fonctions propres de la covariance, mais au détriment de l’interprétation physique de la variable \(f\) dont rien n’assure qu’il s’agisse d’une fréquence au sens de Fourier. Un compromis a néanmoins été proposé en 1965 par Maurice B. Priestley [50], en restreignant le cadre d’analyse aux processus dits “oscillants”, c’est-à-dire tels que \(\psi(t,f)\) soit de la forme d’une exponentielle complexe classique modulée par une fonction \(a(t,f)\) supposée à évolution lente. Il en résulte un “spectre évolutif” (de Priestley) défini par \(P(t,f) = |a(t,f)|^2\,\Gamma(f)\), dont l’estimateur proposé est essentiellement un spectrogramme.

4. Vers le paysage actuel

À la différence de la mécanique quantique où la distribution de Wigner, sans occuper le devant de la scène, obtint au fil des ans une reconnaissance et une forme continue d’intérêt du fait des liens qu’elle entretenait avec le problème de la quantification, la distribution de Ville resta longtemps lettre morte et elle ne refit véritablement surface qu’à fin des années 70. À l’échelle nationale, Bernard Escudié fut son promoteur principal mais, au niveau international, c’est la série des trois articles de Theo A.C.M. Claasen et Wolfgang F.G. Mecklenbraüker [10, 11, 12] qui déclencha un engouement pour le sujet et une vague de travaux dans les années 80, dans des directions aussi variées que la rationalisation du choix des fonctions de paramétrisation, la géométrie des distributions, la généralisation des classes “à la Cohen”, l’adaptativité, l’extension à des dimensions et/ou des ordres supérieurs, l’amélioration de la localisation, etc.

Les conférences internationales virent se multiplier les sessions spéciales dédiées, la première se tenant à San Diego, lors du congrès IEEE-ICASSP de 1984, et une série d’autres se réunissant annuellement lors du congrès d’été SPIE, à San Diego toujours. L’IEEE Signal Processing Society créa un symposium biennal “Time-Frequency and Time-Scale” qui fut organisé successivement à Victoria (1992), Philadelphie (1994), Paris (1996) et Pittsburgh (1998). Des articles de synthèse [16, 31] et des ouvrages [21, 14, 30, 7] apparurent, et c’est vers ceux-ci qu’il faut se tourner pour connaître ce qui ne relève plus tant de l’histoire que de l’évolution de l’état de l’art⁶.

Références

[1] C. d’Alessandro et C. Demars, “Représentation Temps-Fréquence du Signal de Parole,” Traitement du Signal, Vol. 9, No. 2, pp. 153-173, 1992.
[2] J.B. Allen and L.R. Rabiner, “A Unified Approach to STFT Analysis and Synthesis,”
Proc. IEEE, Vol. 65, pp. 1558-1564, 1977.
[3] R. Balian, “Un Principe d’Incertitude Fort en Théorie du Signal ou en Mécanique Quantique,” C. R. Acad. Sc. Paris II, Vol. 292, No. 20, pp. 1357-1362, 1981.
[4] M. Basseville, P. Flandrin et N. Martin (eds.), “Signaux Non Stationnaires : Ana- lyses Temps-Fréquence et Segmentation - Fiches Descriptives d’Algorithmes,” Traitement du Signal, Suppl. Vol. 9, No. 1, pp. 77-147, 1992.
[5] M.J. Bastiaans, “Gabor’s Expansion of a Signal into Gaussian Elementary Signals,”
Proc. IEEE, Vol. 68, No. 4, pp. 538-539, 1980.
[6] A. Blanc-Lapierre et B. Picinbono, “Remarques sur la Notion de Spectre Instantané de Puissance”, Publ. Sci. Univ. d’Alger B, Vol. 1, pp. 2-32, 1955.
[7] B. Boashash (ed.), Time-Frequency Signal Analysis and Processing — A Compre- hensive Reference (2nd Ed.), Elsevier, 2015.
[8] G. Bonnet, “Considérations sur la Représentation et l’Analyse Harmonique des Signaux Déterministes ou Aléatoires,” Ann. Télécom., Vol. 23, No. 3-4, pp. 62-86, 1968.
[9] B. Burke-Hubbard, Ondes et Ondelettes — La Saga d’un Outil Mathématique, Belin, Paris, 1995.
[10] T.A.C.M. Claasen and W.F.G. Mecklenbraüker, “The Wigner Distribution — A Tool for Time-Frequency Signal Analysis — Part I : Continuous-Time Signals,” Philips J. Res., Vol. 35, No. 3, pp. 217-250, 1980.
[11] T.A.C.M. Claasen and W.F.G. Mecklenbraüker, “The Wigner Distribution — A Tool for Time-Frequency Signal Analysis — Part II : Discrete-Time Signals,” Philips J. Res., Vol. 35, No. 4/5, pp. 276-300, 1980.
[12] T.A.C.M. Claasen and W.F.G. Mecklenbraüker, “The Wigner Distribution — A Tool for Time-Frequency Signal Analysis — Part III : Relations with Other Time- Frequency Signal Transformations,” Philips J. Res., Vol. 35, No. 6, pp. 372-389, 1980.
[13] L. Cohen, “Generalized Phase-Space Distribution Functions,” J. Math. Phys., Vol. 7, No. 5, pp. 781-786, 1966.
[14] L. Cohen, Time-Frequency Analysis, Prentice-Hall, Englewood Cliffs, 1995.
[15] L. Cohen, “A General Approach for Obtaining Joint Representations in Signal Analysis. I. Characteristic Function Operator Method,” IEEE Trans. on Signal Proc., Vol. 44, No. 5, pp. 1080-1090, 1996.
[16] L. Cohen, “Time-Frequency Distributions — A Review,” Proc. IEEE, Vol. 77, No. 7, pp. 941-981, 1989.
[17] L. Cohen and Y.L. Zaparovanny, “Positive Quantum Joint Distributions,” J. Math. Phys., Vol. 21, No. 4, pp. 794-796, 1980.
[18] J. Dhombres et J.-B. Robert, Fourier, Créateur de la Physique Mathématique, Belin, Paris, 1998.
[19] B. Escudié, C. Gazanhes, Henri Tachoire et Vincenç Torra, Des Cordes aux Onde- lettes. Publications de l’université de Provence, 2002.
[20] B. Escudié et J. Gréa, “Représentation Hilbertienne et Représentation Conjointe en Temps et Fréquence des Signaux d’Énergie Finie, Interprétation Physique en Fonction des Observations,” VIème Coll. GRETSI sur le Traitement du Signal et ses Applications, pp. 5/1-5/6, Nice, 1977.
[21] P. Flandrin, Temps-Fréquence, Hermès, Paris, 1993.
[22] G.B. Folland, Harmonic Analysis in Phase Space, Ann. of Math. Studies No. 122, Princeton Univ. Press, Princeton, 1989.
[23] J. Fourier, Théorie Analytique de la Chaleur, Firmin Didot, Paris, 1822.
[24] D. Gabor, “Theory of Communication,” J. IEE, Vol. 93, No. 11, pp. 429-457, 1946.
[25] M.T. Heideman, D.H. Johnson, and C.S. Burrus, “Gauss and the History of the Fast Fourier Transform,” IEEE ASSP Mag., Vol. 1, No. 4, pp. 14-21, 1984.
[26] G. Gambardella, “Time-Scaling and Short-Time Spectral Analysis,”, J. Acoust. Soc. Amer., Vol. 44, No. 6, pp. 1745-1747, 1968.
[27] R.J. Glauber, “Coherent and Incoherent States of the Radiation Field,” Phys. Rev., Vol. 131, No. 6, pp. 2766-2788, 1963.
[28] W. Heisenberg, “Über den anschaulichen Inhalt der quantentheoretischen Kinema- tik und Mechanik,” Zeitschrift für Physik, Vol. 43, No.3-4, pp. 172-198, 1927.
[29] C.W. Helström, “An Expansion of a Signal in Gaussian Elementary Signals,” IEEE Trans. on Info. Theory, Vol. IT-12, pp. 81-82, 1968.
[30] F. Hlawatsch et F. Auger (eds.), Temps-Fréquence — Concepts et Outils, Lavoisier, Paris, 2005.
[31] F. Hlawatsch and G.F. Boudreaux-Bartels, “Linear and Quadratic Time-Frequency Signal Representations,” IEEE Signal Proc. Mag., Vol. 9, No. 2, pp. 21-67, 1992.
[32] L. Hörmander, The Analysis of Linear Partial Differential Operators, Springer- Verlag, 1983-1985.
[33] R.L. Hudson, “When is the Wigner Quasi-Probability Non-Negative?,” Rep. Math. Phys., Vol. 6, pp. 249-252, 1974.
[34] K. Husimi, “Some Formal Properties of the Density Matrix,” Proc. Phys. Math. Soc. Jpn., Vol. 22, pp. 264-314, 1940.
[35] J.R. Klauder and B. Skagerstam, Coherent States, World Scientific, Singapore, 1985.
[36] W. Koenig, H. K. Dunn, and L. Y. Lacy, “The Sound Spectrograph,” J. Acoust. Soc. Amer., Vol. 18, pp. 19-49, 1946.
[37] J.G. Krüger and A. Poffyn, “Quantum Mechanics in Phase-Space, I. Unicity of the Wigner Distribution,” Physica, Vol. 85A, pp. 84-100, 1976.
[38] V.V. Kuryshkin, “La Mécanique Quantique avec une Fonction Non-Négative de Distribution dans l’Espace des Phases,” Ann. Inst. Henri Poincaré, Vol. XVII, No. 1, pp. 81-95, 1972.
[39] J.-L. Lacoume et W. Kofman, “Étude des Signaux Non Stationnaires par la Re- présentation en Temps et en Fréquence,” Ann. Télécom., Vol. 30, pp. 231-238, 1975.
[40] M.J. Levin, “Instantaneous Spectra and Ambiguity Functions,” IEEE Trans. on Info. Theory, Vol. IT-13, pp. 95-97, 1967.
[41] E. Marie et E. Cerisier, Les Oscillations de Joseph Fourier, Petit à Petit, 2018.
[42] W. Martin and P. Flandrin, “Wigner-Ville Spectral Analysis of Nonstationary Processes,” IEEE Trans. on Acoust., Speech and Signal Proc., Vol. ASSP-33, No. 6, pp. 1461-1470, 1985.
[43] Y. Meyer, Les Ondelettes — Algorithmes et Applications, Armand Colin, Paris, 1992.
[44] L.K. Montgomery and I.S. Reed, “A Generalization of the Gabor-Helström Trans- form,” IEEE Trans. on Info. Theory, Vol. IT-13, pp. 344-345, 1967.
[45] C.H. Page, “Instantaneous Power Spectra,” J. Appl. Phys., Vol. 23, pp. 103-106, 1962.
[46] L. Pimonow, Vibrations en Régime Transitoire, Dunod, Paris, 1962.
[47] M.R. Portnoff, “Time-Frequency Representations of Signals and Systems Based on Short-Time Fourier Analysis,” IEEE Trans. on Acoust., Speech and Signal Proc., Vol. ASSP-28, No. 1, pp. 55-69, 1980.
[48] R. K. Potter, “Visible Patterns of Sound,” Science, Vol. 102, pp. 463-470, 1945.
[49] R.K. Potter, G.A. Kopp, and H.C. Green, Visible Speech, D. van Nostrand, New York, 1947.
[50] M.B. Priestley, “Evolutionary Spectra and Non-Stationary Processes,” J. Roy. Stat. Soc. B, Vol. 27, No. 2, pp. 204-237, 1965.
[51] A.W. Rihaczek, “Signal Energy Distribution in Time and Frequency,” IEEE Trans. on Info. Theory, Vol. IT-14, No. 3, pp. 369-374, 1968.
[52] A.W. Rihaczek, Principles of High-Resolution Radar, McGraw-Hill, New York, 1969.
[53] C.E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, Vol. 27, pp. 379-423 and 623-656, 1948.
[54] M. Springborg, “Phase Space Functions and Correspondence Rules,” J. Phys. A, Vol. 16, pp. 535-542, 1983.
[55] J. Ville, “Théorie et Applications de la Notion de Signal Analytique,” Câbles et Transmissions, 2ème A., No. 1, pp. 61-74, 1948.
[56] H. Weyl, “Quantenmechanik und Gruppentheorie,” Zeitschrift für Physik, Vol. 46, pp. 1-46, 1927.
[57] H. Weyl, Gruppentheorie und Quantenmechanik, S. Hirzel, Leipzig, 1928.
[58] N. Wiener, Cybernetics, or Control and Communication in the Animal and the Machine, The MIT Press, Cambridge, 1948.
[59] E.P. Wigner, “On the Quantum Correction for Thermodynamic Equilibrium,” Phys. Rev., Vol. 40, pp. 749-759, 1932.
[60] E.P. Wigner, “Quantum-Mechanical Distribution Functions Revisited,” in Perspec- tives in Quantum Theory, W. Yourgrau and A. van der Merwe (eds.), Dover, New York, 1971.
[61] P.M. Woodward, Probability and Information Theory with Application to Radar, Pergamon Press, London, 1953.
[62] http://perso.ens-lyon.fr/patrick.flandrin/Fourier250/
[63] https://youtu.be/oda1BFBK3pY
[64] https://gallica.bnf.fr/ark:/12148/bpt6k5688601m/f5.image.texteImage
[65] https://www.youtube.com/watch?v=6LzSIQbSX1U
[66] https://griffonagedotcom.wordpress.com/2018/07/26/the-secret-military-origins-of-the-sound-spectrograph

Notes

^1. Cette perspective est bien sûr restrictive dans la mesure où les idées même de Fourier ne sont pas sorties de nulle part et qu’un long cheminement a conduit aux concepts qui nous sont devenus familiers : la référence [19] est particulièrement instructive à cet égard.

^2. On pourra se reporter à [25] pour une approche historique sur les algorithmes de transformation rapide de Fourier et les travaux précurseurs conduits, en particulier par Carl Friedrich Gauss au XIXème siècle, avant l’article classique de James W. Cooley et John W. Tukey en 1965.

^3. Ironiquement, c’est en essayant de prouver un résultat de même nature pour le maillage dyadique qu’Yves Meyer construisit la première base orthonormée d’ondelettes.

^4. Pour une quantité \(G(q, p)\) donnée, l’opérateur associé \(G\) est fonctionnellement dépendant des opérateurs élémentaires \(q\) et \(p\) associés à la position \(q\) et l’impulsion \(p\), et définis par leurs actions respectives \(({\bf q}\psi)(q) = q\psi(q)\) et \(({\bf p}\psi)(q) = -i\hbar (\partial \psi /\partial q)(q)\). Ces deux opérateurs élémentaires ne commutant pas, la “règle de correspondance” \(G(q,p) \rightarrow {\bf G}({\bf q},{\bf p})\) n’est pas unique.

^5. On notera que, dans l’article original [59], l’introduction de la définition proposée est assortie de l’énigmatique note de bas de page “This expression was found by L. Szilard and the present author some years ago for another purpose”. . . À notre connaissance, il n’existe pas trace du quand et du pourquoi de cette antériorité.

^6. Une mention particulière pourra être faite à l’effort comparatif conduit collectivement au sein du GRECO CNRS “Traitement du Signal et Images” dans le cadre d’un de ses groupes de travail [4].